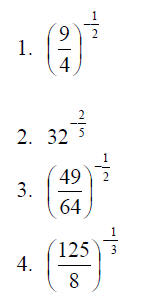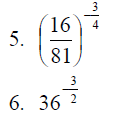Worksheet on rational exponents

Recall that for a rational exponent, the numerator means the power and the denominator means the root.
So, for example: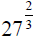 means

a) The cube root of 27 squared, or
b) The square of the cube root of twenty-seven.
a) 27 squared is 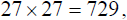, and the cube root of 729 (sometimes written 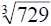) is 9, which you find either using the calculator or by realizing that
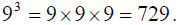
b) The cube root of 27 is 3 (because 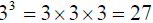), and .

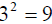In either case we see that 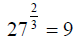, although taking the root first is usually easier if for no other reason than the numbers are smaller.

Compute the following numbers:

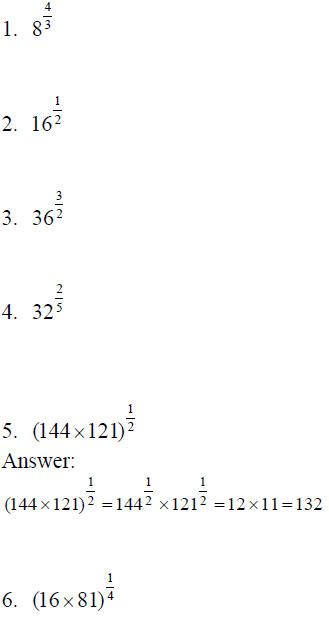
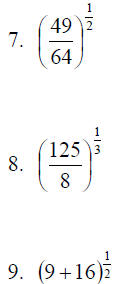
Here you must first add, then take the square root.

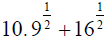
Here you take the square roots first, then add.

11. Which answer is bigger, the sum of the square roots (#10) or the square root of the sum (#9)? Why?

To annoy you further, we can also have negative exponents as well as positive ones. This is not such a big deal if we remember that a negative

exponent just means the reciprocal. For example: 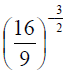looks bad, but if we tease out the meaning it is comprehensible. The exponent has three parts:

a) a minus sign,
b) a 2 in the denominator
c) a 3 in the numerator. In turn they mean
a) the reciprocal, b) the square root, and c) the cube (the third power).
Taking care of these, one at a time we get:

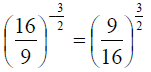(taking the reciprocal gets rid of the pesky

minus sign in the exponent) 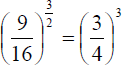(taking the square root gets rid of the 2 in the denominator, and finally

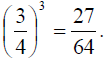Not so bad.

Compute: