Math 103 Problem Set #2 Solution

(The propositional symbols and predicates should be obvious.)

Section 1.5, exercises on pp.72 - 74

1. (Exercise 6)
Use rules of inference to show that the hypotheses “If it does not rain or if it is not foggy, then the sailing
race will be held and the lifesaving demonstration will go on,” “If the sailing race is held, then the trophy
will be awarded,” and “The trophy was not awarded” imply the conclusion “It rained.”

2. (Exercise 16)
For each of these arguments determine whether the argument is correct or incorrect. If incorrect, explain
why. If correct, provide a proof in the style of.
a) Everyone enrolled in the university has lived in a dormitory. Mia has never lived in a dormitory.
Therefore, Mia is not enrolled in the university.
b) A convertible car is fun to drive. Isaac’s car is not a convertible. Therefore, Isaac’s car is not fun to
drive.
c) Quincy likes all action movies. Quincy likes the movie Eight Men Out. Therefore, Eight Men Out is
an action movie.
d) All lobstermen set at least a dozen traps. Hamilton is a lobsterman. Therefore, Hamilton sets at
least a dozen traps.

Something got cut off in the instructions. In should say "in the
style of examples 12 and 13".

(a)
1. 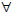x(U(x) → D(x))
2. ¬D(Maria)
----------------------
3. ¬U(Maria) Universal modus tollens, 1, 2 (see p. 72)
or, in more detail
3. U(Maria) → D(Maria) Univ. instantiation, 1
4. ¬U(Maria) Modus tollens, 2, 3

(b) Incorrect. Issac's car might be not a convertible and fun to
drive. The premises would still be true, but the conclusion would be
false.

(c) Incorrect. Eight Men Out could be not an action movie and the
premises would still be true.

(d) Correct. This is just a Universal Modus Ponens (p. 71), or it
could be spelled out.

3. (Exercise 28)
Use rules of inference to show that if 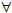x(P(x) 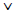Q(x)) and 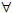x((¬ P(x) 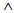Q(x)) → R(x)) are true, then
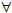x(¬ R(x) → P(x)) is also true, where the domains of all quantifiers are the same.

There is a shortcut or two in the above, e.g., 7 to 8, but these are
allowed if obvious.

4. (Exercise 34)
The Logic Problem, taken from WFF’N PROOF, The Game of Logic, has these two assumptions:
1. “Logic is difficult or not many students like logic.”
2. “If mathematics is easy, then logic is not difficult.”
By translating these assumptions into statements involving propositional variables and logical
connectives, deter-mine whether each of the following are valid conclusions of these assumptions:
a) That mathematics is not easy, if many students like logic.
b) That not many students like logic, if mathematics is not easy.
c) That mathematics is not easy or logic is difficult.
d) That logic is not difficult or mathematics is not easy.
e) That if not many students like logic, then either mathematics is not easy or logic is not difficult.

Use the following symbols:
LD = "Logic is difficult"
MS = "Many students like logic"
ME = "Mathematics is easy"

Assumptions:
1. LD 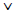¬MS
2. ME → ¬LD
(a) To prove: MS → ¬ME

3. ¬ME 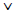¬LD 2, Table 7
4. ¬MS 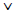¬ME 1, 3 Resolution
5. MS → ¬ME 4, Table 7

(b) To prove: ¬ME → ¬MS
This is not a valid conclusion. This would be vacuously true if we were
sure that ME was true, OR if we were sure that MS was false. But the
premises tell us neither of these.

(C) To prove: ¬ME 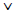LD
This is not a valid conclusion. If it were, doing resolution with 3
above would mean that ¬ME was true, and we do not know that from the
premises.

(d) To prove: ¬LD 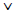¬ME
This is 3 above.

(e) To prove: ¬MS → (¬ME 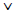¬LD) Note that we translate "either/or" as
inclusive "or". Sometimes the meaning in English is exclusive "or",
but we will only do that when it says "either ... or ... but not both".
3. ¬ME 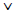¬LD 2, Table 7 (as above)
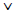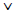4. MS (¬ME ¬LD) 3, Addition
5. ¬MS → (¬ME 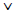¬LD) 4, Table 7

5. (Exercise 8)
Prove that if n is a perfect square, then n + 2 is not a perfect square. Give a proof in paragraph style,
similar to Example 1, p. 77.

The domain isn't completely clear: should we consider 0 a perfect
square? Let's say we do. Then we'll consider two cases:

Case 1: n = 0.
Then n + 2 = 2, which is not a perfect square.

Case 2: n ≥ 1.
Suppose that n is a perfect square, i.e., that there exists an integer
m such that n = m². Since n ≥ 1, we have m ≥ 1. Then the next perfect
square after n would be (m+1)² = m² + 2m + 1 = n + 2m + 1. But this is
at least n + 3. Since all other perfect squares are even greater,
n + 2 is less than all perfect squares greater than n, so n + 2 is not
a perfect square.

6. (Exercise 18)
Prove that if n is an integer and 3n + 2 is even, then n is even. In Rosen, you are asked to prove this two
ways. For this assignment, give one proof, done however you wish. Give your proof in paragraph style.

We will assume the domain is non-negative integers, and prove the
contrapositive: if n is odd, then 3n + 2 is odd. If n is odd, there
exists an integer k such that n = 2k + 1. So
3n + 2 = 3(2k + 1) + 2
= 6k + 3 + 2
= 2(3k + 2) + 1
which is odd.

A proof by contradiction is about the same. Suppose 3n + 2 is even and
then suppose that n is odd. We get 3n + 2 = an odd number as above,
which contradicts the hypothesis that 3n + 2 is even. So n is even.

[Another argument starts like this: "if 3n + 2 is even, then 3n is
even". Saying "so n is even" would be considered too much of a leap.
It needs to be shown.]

7. (Exercise 36)
Show that the propositions p₁, p₂, p₃, and p₄ can be shown to be equivalent by showing that p₁ ↔ p₄,
p₂ ↔ p₃, and p₁ ↔ p₃. Give a proof in paragraph style. You may include a diagram as part of your
proof.

Suppose we prove the indicated biconditionals. We would have

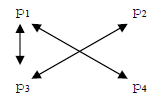
From this we see
that p₁ → p₃ → p₂
and p₂ → p₃ → p₁
so p₁ ↔ p₂

In a similar manner, we can see that
p₂ ↔ p₄ and p₃ ↔ p₄.

8. (Exercise 34)
Prove that between every rational number and every irrational number there is an irrational number.
Give a proof in paragraph style.

Suppose r is a rational number and that i is an irrational number such
that i > r. Let n = (r + i) / 2, and suppose that n is rational.
Then i = 2n – r. But since r and n are rational, that would be a
rational number, contradicting the assumption about i. Thus taking
the midpoint between a rational and irrational is one way to find an
irrational between them. (The argument also works if i < r.)

9. (Exercise 14)
Let P(x) be the statement “student x knows calculus” and let Q(y) be the statement “class y contains a
student who knows calculus.” Express each of these as quantifications of P(x) and Q(y).

a) Some students know calculus.
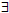xQ(x)

b) Not every student knows calculus.
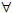¬xQ(x)

c) Every class has a student in it who knows calculus.
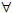yQ(y)

d) Every student in every class knows calculus.
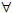xP(x) [If there are students not in classes, this says too much.
But P and Q are all we have.]

e) There is at least one class with no students who know calculus.
[How do we say this? I think we need a predicate I(x,y) that
means student x is in class y to do (d) and (e) properly.]

10. (Exercise 18)
Translate the following statement into first order logic: “No one has more than two grandmothers.” Use
the propositional function G(x, y), to represent “x is the grandmother of y.” Note: in Rosen, it says "three"
rather than "two".

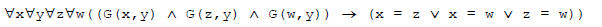
Note: You will find Errata for the Rosen book at:
A few of these are relevant.