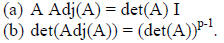MATH 317 MID-TERM EXAM

Note:
[1] There should be two parts.
[2] Read the questions carefully before answering.
[3] Show all your work to receive credit.

PART A (15 points)
State true or false or fill in the blanks with appropriate answers, for each of the following
statement (assume all matrix operations are valid).

(1) When both A and B are nonsingular (AB)^-1 = B^-1 A^-1.
(2) A is nonsingular if and only if det(A) is nonzero.
(3) Rank (AB) is always equal to rank of A.
(4) det(A + B) = det(A) + det(B).
(5) If A and B are square matrices, then det(AB) = det(A)det(B).
(6) When A inverse exists, det(A^-1) = 1/det(A).
(7) A square matrix A is said to be skew-symmetric iff
(8) The system Ax = b will have solution iff rank (A) = rank[A b].
(9) It is possible for the system Ax = 0 to be inconsistent.
(10) W = {(x,0)^T: x is a real number} is a subspace of R² with standard operations.
(11) V = {set of all 3 × 3 nonsingular matrices} is a subspace of the set of all 3 x 3 matrices with
standard operations.
(12) For the
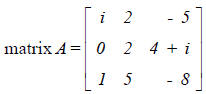the trace is___ and the determinant is
(13) Suppose that x is a nonzero vector. Then Ax = 0 iff A is singular.
(14) A Adj(A) = det(A) I is always true when and only when A is nonsingular.
(15) It is possible for a p x q matrix A to have neither a left- nor a right-inverse.

PART B (85 points)
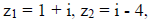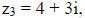[1] Given and find

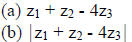
(c) the complex conjugate of
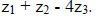
[2] Show that for all complex numbers z and w
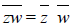
[3] Suppose that A and B are p x p matrices such that AB is nonsingular. Show that A and B both
are nonsingular.
[4] Show that B is row-equivalent to A. Show that there exists a nonsingular matrix F such that
FA = B.
[5] Solve the system of linear equations AX = B, where A, X, and B are given by

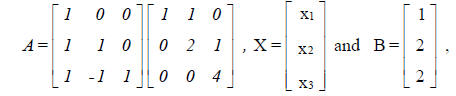
[6] Show that every Hermitian matrix is the sum of a real symmetric matrix and i times a real
skew-symmetric matrix.
[7] Suppose that A is a nonsingular matrix of order 3, reduced to an identity matrix by
performing the following elementary row operations (in the same order): (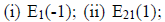
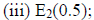Find the matrix A^-1, by first writing A as a product of elementary matrices.
[8] Suppose that B is p x q and A is a p x p nonsingular matrix. Show that the rank of AB equals
the rank of B.
[9] Given the matrix

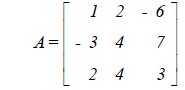
find the LU decomposition of A
[10] If A is a square matrix of order p, show that