EE363 homework

1. Lyapunov condition for passivity. The system described by
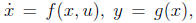
x(0) = 0, with u(t), y(t) ∈ R^m, is said to be passive if

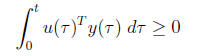
holds for all trajectories of the system, and for all t.

Here we interpret u and y as power-conjugate quantities (i.e., quantities whose product
gives power) such as voltage and current or force and velocity. The inequality
above states that at all times, the total energy delivered to the system since t = 0 is
nonnegative, i.e., it is impossible to extract any energy from a passive system.

(a) Establish the following Lyapunov condition for passivity: If there exists a function
V such that V (z) ≥ 0 for all z, V (0) = 0, and 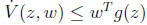for all w and z,
then the system is passive.

(b) Now suppose the system is 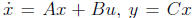, and consider the quadratic
Lyapunov function V (z) = z^TPz. Express the conditions found in part (a) as a
matrix inequality involving A, B, C, and P.

Remark: you will not be surprised to learn that for a linear system, the condition
you found in this problem is not only sufficient but also necessary for the system to
be passive. This result is called the Kalman-Yakubovich-Popov (KYP) or positive
real (PR) lemma.

(c) Now consider the specific case with

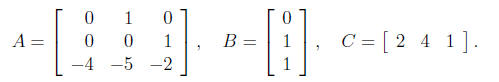
Use an LMI solver to find a matrix P for which the Lyapunov function V (z) =
z^TPz establishes passivity of the system.

2. Finding a discrete-time diagonal Lyapunov function. Recall problem 4 from the last
homework, which concerned the stability of a digital filter with saturation. In that
problem you proved that the system x_t+1 = sat(Ax_t) is globally asymptotically stable
if there exists a nonsingular diagonal D such that ||DAD^-1||< 1.

(a) Show how to find a nonsingular diagonal D that satisfies ||DAD^-1|| < 1, or
determine that no such D exists, using LMIs.
Hints:

• A matrix Z satisfies |Z| < 1 if and only if Z^TZ < I.
• You might find it easier to search for E = D^2, which is positive and diagonal.

(b) Use an LMI solver to find such a D for the specific case

3. Finding a stabilizing state feedback via LMIs. We consider the time-varying LDS

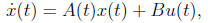
with x(t) ∈ Rⁿ and u(t) ∈ R^m, where A(t) ∈ {A₁, . . . ,A_M}. Thus, the dynamics
matrix A(t) can take any of M values, at any time. We seek a linear state feedback
gain matrix K ∈ R^m×n for which the closed-loop system

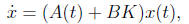
is globally asymptotically stable. But even if you’re given a specific state feedack gain
matrix K, this is very hard to determine. So we’ll require the existence of a quadratic
Lyapunov function that establishes exponential stability of the closed-loop system, i.e.,
a matrix P = P^T > 0 for which

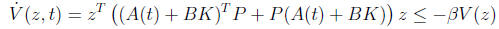
for all z, and for any possible value of A(t). (The parameter β > 0 is given, and sets
a minimum decay rate for the closed-loop trajectories.)

So roughly speaking we seek
• a stabilizing state feedback gain, and
• a quadratic Lyapunov function that certifies the closed-loop performance.

In this problem, you will use LMIs to find both K and P, simultaneously.

(a) Pose the problem of finding P and K as an LMI problem.
Hint: Starting from the inequality above, you won’t get an LMI in the variables
P and K (although you’ll have a set of matrix inequalities that are affine in K,
for fixed P, and linear in P, for fixed K). Use the new variables X = P^-1 and
Y = KP^-1. Be sure to explain why you can change variables.

(b) Carry out your method for the specific problem instance

B = (1, 0, 0), and β = 1. (Thus, we require a closed-loop decay at least as fast as e^−t/2.)

4. Stability of a switching system. We consider the nonlinear dynamical system

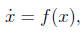
where

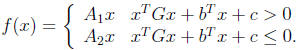
You can assume that c > 0. Roughly speaking, the system switches between two linear
dynamical systems, depending on the sign of a quadratic function of the state. The
function f can be discontinuous, but don’t let it worry you.

We seek a positive definite quadratic Lyapunov function V (x) = x^TPx for which
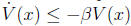for all x. (The parameter β is given.)

(a) Explain how to find such a P, or determine that no such P exists, by formulating the problem as an LMI.
(b) Use an LMI solver to find such a P for the specific case

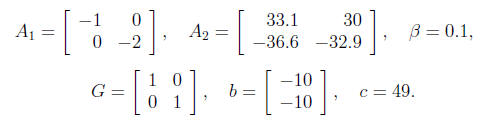
5. Perron-Frobenius theorem for nonnegative but not regular matrices. Suppose A ∈ R^n×n
and is nonnegative, with Perron-Frobenius eigenvalue λ_pf . Show by examples that the
following can occur:

(a) The multiplicity of λ_pf can exceed one.
(b) The eigenvalue λ_pf is associated with a Jordan block of size larger than 1 × 1.
(c) There are multiple PF eigenvectors, i.e., there are nonzero nonnegative vectors v
and 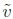, not multiples of each others, such that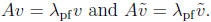

(None of these can occur if A is regular, i.e., A^k > 0 for some k.)

6. A bound on the Perron-Frobenius eigenvalue. Let A ≥ 0, with PF eigenvalue λ_pf . Show
that

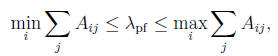
i.e., λ_pf lies between the minimum and maximum of all row sums of A. Show that the
same holds for the column sums.

7. Some relations between a matrix and its absolute value. In this problem, A ∈ R^n×n,
and |A| denotes the matrix with entries |A|_ij = |A_ij|.

For each of the following statements, give a proof of the statement or provide a specific
counterexample.

(a) If all eigenvalues of |A| have magnitude less than one, then all eigenvalues of A
have magnitude less than one.
(b) If all eigenvalues of A have magnitude less than one, then all eigenvalues of |A|
have magnitude less than one.
(c) If 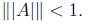then
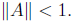
(d) If 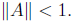then

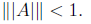
8. A weighted maximum Lyapunov function. Suppose A is nonnegative, regular, and
stable, and let v be the PF eigenvector of A, and λ_pf the PF eigenvalue. Consider the
Lyapunov function

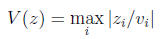
and the system 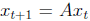. Show that along trajectories of this system, V decreases
at each step by at least the factor λ_pf .

9. Iterative power control with receiver noise. We consider the power control problem
described in the lecture, with one modification: we include a receiver noise term, so
the signal to interference plus noise ratio (SINR) is

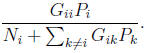
Note that by increasing the powers of all transmitters, we can make the effects of the
noise on the SINR small, so we can achieve a minimum SINR as close as we like (but
not equal) to the optimal SIR when there is no noise.

Now suppose the following iterative power control scheme is used to set the powers:
at each step of the iteration, the power P_i is adjusted to that the SINR of receiver i
would equal γ, provided the other powers are not changed.

Show that this scheme works, provided 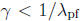, where λ_pf is the PF eigenvalue of
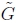(‘Works’ means the powers converge to a power allocation for which each SINR is
equal to γ). You can assume that G_ij > 0, and that N_i > 0.