Introductory Mathematics Concept Guide

5. Significant Figures

The precision of a measurement indicates how well several determinations of the same quantity agree. In the
laboratory, chemists attempt to set up experiments so that the greatest possible accuracy can be achieved. For
each individual experiment, several measurements are usually made and their precision determined. Usually,
better precision is taken as an indication of better experimental work. A calculated result can be no more precise
than the least precise piece of information that went into the calculation. This is why the rules of significant
figures are used.

Rule 1

To determine the number of significant figures in a number, read the number from left to right and count all the
digits, starting with the first digit that is not zero. If the last digit of a number does not contain a decimal point,
then the number of significant figures is equal to the number of non-zero digits in the number. Zeros to the left
of 1 only locate the decimal point. This is clearer when it is written in scientific notation.

Rule 2

When adding or subtracting, the number of decimal places in the answer should be equal to the number of
decimal places in the number with the fewest places.

Rule 3

When multiplying or dividing, the number of significant figures in the answer should be the same as the number
with the fewest significant figures.

Rule 4

When a number is rounded off (the number of significant figures is reduced), the last digit is increased by 1
only if the following digit is 5 or greater. When calculating, you should do the calculation using all of the digits
allowed by the calculator and round off only at the end of the problem. Rounding off in the middle of the
problem can cause errors.

Question

How many significant figures are there in the numbers
?

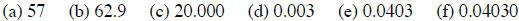Solution
(a) Beginning with the 5 and counting gives two significant figures.
(b) Beginning count with the 6 gives three significant figures.
(c) All zeros here are significant. There are five significant figures.
(d) None of the zeros here are significant, giving one significant figure.
(e) The zeros to the left are insignificant, but the zero in the middle is a significant digit, giving three
significant figures.
(f) The zero at the end and the zero in the middle are significant digits, giving four significant figures.

Problem
Perform the following calculations and express the answers to the proper number of significant figures:


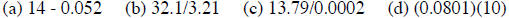
Solution


(Note: the exact factor of 10 does not limit the number of significant figures in the answer.)

6. Percents and Fractions

Fractions
A fraction is a part of a whole. In its simplest form, the value of a fraction is less than one. An example
commonly used to explain fractions is a pie: cut the pie into eight slices, then eat two. Two-eighths of the pie is
gone. There are six pieces left, so six-eighths (6/8) of the pie is left.

a. Reducing Fractions

Imagine you have three pies cut into sections: one into fourths, one into eighths, and one into sixteenths. Take
one piece from the first pie, two from the second, and four from the third. How much has been eaten from each
pie? From pie one: one-fourth (1/4), from pie two: two eighths (2/8), and from pie three: four-sixteenths (4/16).
The same amount, however, has been taken from each pie: one quarter (1/4). As you can see, it is frequently
more convenient to talk about fractions in the most reduced, or simplest terms.

To reduce a fraction:
1. Find a number that divides evenly into the numerator and the denominator.
2. Check to see if another number goes in evenly. Repeat until the fraction is reduced as far as possible.
Example: 48/64
(48/8)/(64/8) = 6/8
(6/2)/(8/2) = 3/4

b. Converting Between Improper Fractions and Whole/ Mixed Numbers
An improper fraction is one in which the numerator is larger than the denominator. For example, if you were
told you had six-fourths (6/4) of a pie left, you would know that you had one whole pie (4/4) plus one-half of a
pie (2/4). It can be more useful to express the fraction as a mixed number, a number containing a whole number
and a fraction. Thus rather than 6/4 of a pie, you have 1 1/2 pies.

To change an improper fraction into a mixed number:
1. Divide the denominator into the numerator.
2. Write the remainder as a fraction over the original denominator.
3. Reduce the remaining fraction.

c. Changing a Mixed Number into an Improper Fraction
When carrying out mathematical operations, it is usually necessary to work with improper fractions rather than
mixed numbers. To change a mixed number into an improper fraction:
1. Multiply the whole number by the denominator.
2. Add the numerator to the product.
3. Place the sum in the numerator, over the original denominator.

d. Multiplying and Dividing Fractions
To multiply fractions, simply multiply the numerators together and multiply the denominators together. When
multiplying fractions, you can cross reduce: reduce as you normally would a fraction, but use the numerator of
one fraction and the denominator of the other. This will save you from having to reduce the fraction product.
When multiplying a fraction by a whole number, write the whole number as a fraction over one, and multiply as
usual.

Example: (15/7) x (3/5)
1. divide both 15 and 5 by 5
2. (3/7) x (3/1) = 9/7
To divide by a fraction, invert the fraction to the right of the division sign and multiply. Example: 1/2 / 1/8
1. (1/2)(8/1) = 8/2 = 4

e. Adding and Subtracting Fractions
Many problems will require mathematic manipulations of fractions. To continue with the pie example, if you
have 3/8 of one pie and 1/4 of another pie, how much pie do you have?

To add or subtract fractions, they must have the same denominator. Then you simply add the numerators. Thus,
we have 3/8 of one pie and 2/8 of another, leaving us with 5/8 of a pie.

If the fractions you want to add do not have a common denominator, you must change one or both of the
fractions. You can do so by multiplying one or more of the fractions by an expression equivalent to one.

f. Decimals
In one of our earlier examples, we determined that a quarter of the pie had been eaten. We expressed one
quarter as a fraction, 1/4. It can also be expressed as a decimal, 0.25, which is read as twenty-five hundredths.
Any fraction can be expressed as a decimal by dividing the numerator by the denominator.

g. Rounding Off

When a fraction's denominator does not divide evenly into the numerator, the decimal equivalent can be long
and too cumbersome to work with. For example, 1/3 = 0.3333333... The decimal is infinite, so we will want to
use an abbreviated version for our records and calculations. An acceptable equivalent, rounded to two decimal
places, is 0.33. When rounding off, increase the last digit retained by one if the following digit is greater than
or equal to 5. Leave the last digit unchanged if the following digit is less than 5.

Percents
The percent symbol (%) means per hundred. 15% is equivalent to 15/100 or 0.15. Thus, when a quarter of our
pie was eaten, 0.25, or 25% was gone. Any percentage may be expressed in decimal form by dividing by 100
and dropping the percent symbol. For example, 52.3% = 52.3/100 = 0.523. To calculate percentage, you must
change the percent to decimal form (divide the percent by 100) and multiply.