Math Problem Set

Problem 1.1. Find an opponent and play a number of games of 2-
spot and 3-spot sprouts. Find out the best strategy that you can for
2-spot sprouts, and write a short essay describing your finding.
This essay should fit on one side of a sheet of paper.
Due Friday, January 16, 2009.

Problem 1.2. Prove that every game of sprouts starting with any
finite number of spots (say with N spots) must eventually end, no
matter how the players play. (Of course they must obey the rules.)
If the game starts with N spots, give an upper bound on the number
of moves in any game.
Due Wednesday, January 21, 2009.

Problem 1.3. Read pages 39 - 51 in our text "An Introduction to
Mathematical Reasoning" and do problems 5.1 to 5.4 on page 51.
Due Monday, January 26, 2009.

Problem 1.4. Prove by induction that
(1/1x3) + 1/(3 x 5) + 1/(5 x 7) + ... + 1/((2n-1) x (2n + 1)) =
n/(2n + 1).
Due Monday, January 26, 2009.

Problem 1.5. The Fibonacci Numbers are the numbers in the
sequence 1,1,2,3,5,8,13,21,34,55,144,189,....
We denote these by f₁ = 1, f₂ = 1, f₃ = 3, f₄ = 5 and
f_n+1 = f_n + f_n-1.

Each Fibonacci number is the sum of the previous two Fibonacci
numbers. There are many patterns in the Fibonacci series.
Notice that

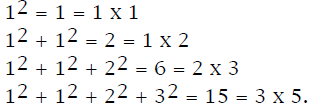
Prove by induction that

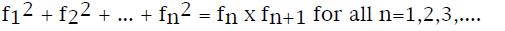
Due Friday, January 30,2009.

Problem 1.6. (Returning to Sprouts) Prove that for every natural
numbrer n (n = 1, 2, 3, 4, ...) there is a sprouts game, starting with
n sprouts, that ends in exaactly 3n -1 moves. You can use
mathematical induction in your proof.

Due Monday, February 2, 2009.

Problem 1.7. In 4-sprouts we use the same rules as in ordinary
sprouts, but we allow 4 lines to touch a spot
as in the diagram below.

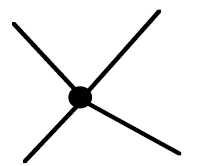
A move has the same form as in regular spots, but notice that the
new spot, having two lines going into it, has two freedoms in the
game of 4-spots. Show that some games of 4-spots can go on forever.
Give specific examples. Think about the question of how to
modify the rules of 4-spots so that it will become a game that always
ends in a finite number of moves.
Due Wednesday, February 4, 2009.

Problem 1.8. The Fibonacci Numbers are the numbers in the
sequence 1,1,2,3,5,8,13,21,34,55,144,189,....
We denote these by f₁ = 1, f₂ = 1, f₃ = 3, f₄ = 5 and
f_n+1 = f_n + f_n-1. We also take f₀ = 0 by convention.
Prove the following formula by induction.

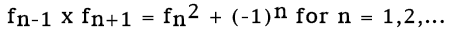
For example 8 x 21 = 168 = 169 - 1 = 13² -1.

Due Friday, February 6,2009.

Problem 1.9. Problem 20. page 56 of our textbook.
Due, Monday, February 9,2009.

Problem 1.9. Problem 20. page 56 of our textbook.
Due, Monday, February 9,2009.

Problem 1.10. Prove by induction that

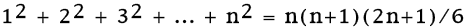
for n = 1,2,3,... .
Due, Monday, February 9,2009.

Problem 1.11. Suppose that you play a sprouts game with n
starting spots and that the game lasts for 3n - 1 moves. How many
Pharisees will there be at the end of the game? Illustrate your result
with a specific example.
Due, Wednesday, February 11,2009.

Problem 1.12. (The Gas-Electricity-Water Problem)
Three companies, the gas company, the electricity compay and the
water company want to make connections from the gas main (G),
the electrical source (E) and the water main (W) to three houses
(H1, H2 and H3). They wish to lay their lines so that no two lines
meet except at the sources (G,E and W) and at the houses
(H1, H2 and H3). Can you find a solution to this design problem?
If not, then why not?

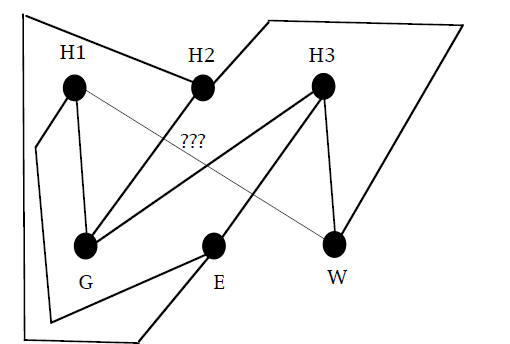
In the illustration above the city planners have drawn a graph to
help them design the connections but they have run into a difficulty
with making a water line from W to H1. Everything went fine with
the design up to that point, but then there does not seem to be any
way to conncet from W to H1 without crossing previously created
lines. It will cost the city a great deal to dig tunnels to make lines
cross over one another. So these designers really need to know
whether the job can be done with no crossovers, and if it cannot be
done that way, then they want to know the least number of
crossovers that are needed to do the job.
Due, Wednesday, February 11,2009.

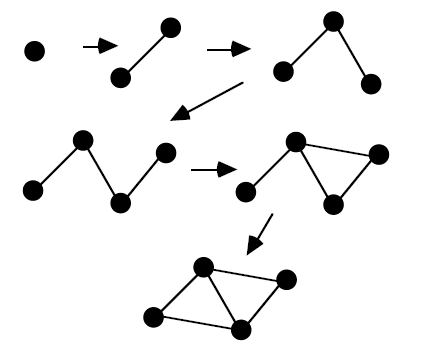
Problem 1.13. Construct a proof of Euler's formula by induction
on the total number of edges and vertices in the graph G. You
should consider how the graph can be built up from simpler graphs
by adding edges to them. In fact, any connected graph can be built
from a single vertex graph by adding new edges in two ways that I
will now explain, but first we introduce an abbreviation: The
diagram below stands for some vertex in a larger graph.

You can tell when I am using this abbreviation because the edges
that go out of this vertex are not meeting any other vertices in the
picuture. The picture is a shorthand for a possibly larger and more
complete picture. In the abbreviation we show three edges touching
the vertex. In a real situation some edges touch the vertex, but the
number is not necessarily equal to three. Ok?

Now lets use this and illustrate two ways to make a larger graph.

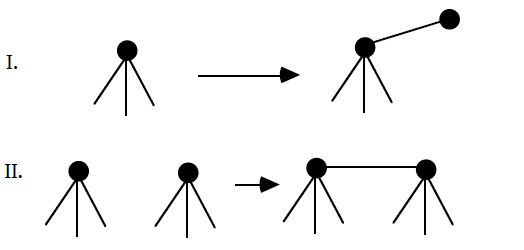
In method number I we add a new edge and a new vertex by
attaching the new edge to an already existing vertex. In method
number II we connect two vertices with a new edge.

Remark. We regard the move

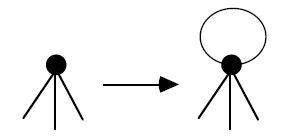
as a special case of II.

I claim that any connected graph can be built up by performing
a sequence of operations of these two types. Here is an example.

You can use this claim in your proof, and if you want, you can also
make a proof of the claim. We will discuss why the claim is true in
class.

Now, to prove the Euler Theorem, you can proceed by induction,
showing that V - E + F does not change its value when you perform a
move of type I or type II. You will find that it is very easy to see this
for type I, and that in order to see it for type II you need
to start with a connected graph. If the graph is connected, then a
move of type II will create a new region in the graph. Look at the
example above and see how this works. You can use this fact also in
your proof (that a move of type II will create a new region). You
should then be able to construct an inductive proof of the Euler
formula.

Here is an example:
We create a triangle graph by adding an edge to a tree.

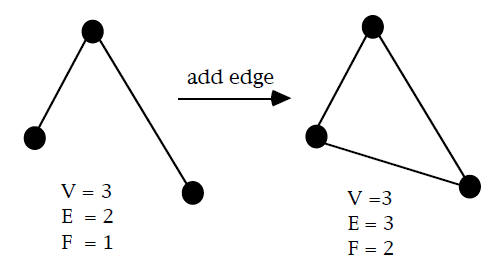
Note that adding the edge creates a new region, and V-E + F does
not change from before to after the addition of the new edge.

(c) Discuss your proof of the Euler formula with another student in
the class. Do you both feel that the proof is complete? What might
be missing? In this problem, it worth having the discussion. We will
discuss some of the issues related to the problem in class before the
problem is due.
Due, Friday, February 20,2009.

Supplement to Problem 1.13.
There is a fact about curves in the plane that you can use in
thinking about regions that are created when graphs are drawn in
the plane.
This fact is called the

Jordan Curve Theorem: A closed curve in the plane without any
self-intersections divides the plane into exactly two regions.

Here is an example:

You are not required to prove this result, but you can use it and it is
interesting to see how complex examples can look!

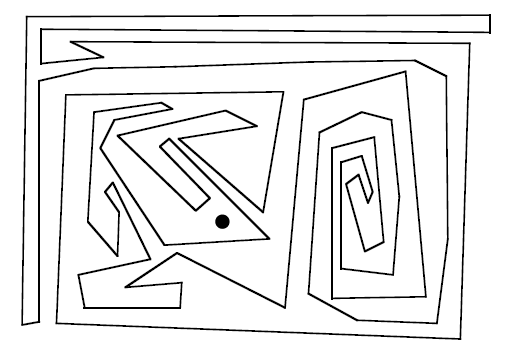
Is the black dot inside or outside this curve?
Of course you can solve this like solving a maze, but look!

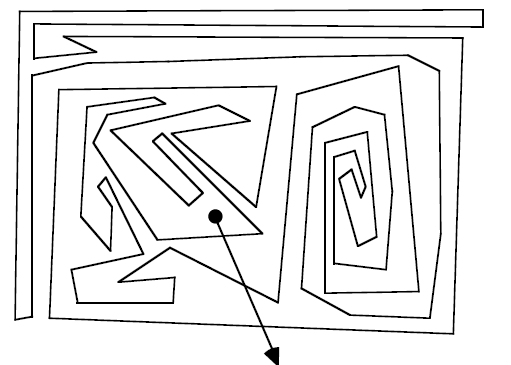
An arrow from the dot intesects the curve in an ODD number of
points. I claim that this tells you that the point must be INSIDE.

If the intersection number were EVEN, then the point would be
outside. Can you explain why this works? (I say explain, and of
course I am hoping that your explanation will turn into a
mathematical proof. But lets explore.)

We will discuss in class why and how the Jordan Curve Theorem is
relevant to proving Euler's Formula.

Remark. Another approach to the Euler formula uses the concept
of a tree: A graph is said to be a tree if it does not contain any cycles
(a cycle is a sequence of distinct edges such that the each edge
shares its endpoints with the edges before and after it in the
sequence. For example in the graph above, bce is a cycle and abcd is
a cycle. When a plane graph has no cycles then the only region it
can delineate is the rest of the plane other than itself, and so a tree
has F = 1.
Show that for a connected tree, V - E = 1.
From this is follows that for connected plane trees V - E + F = 2,
and so we know the Euler formula already for trees.

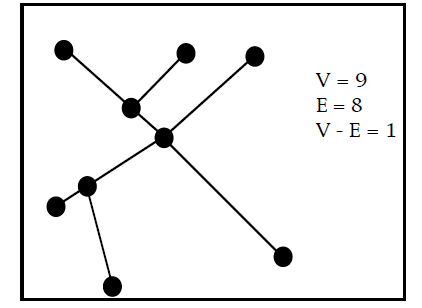
The picture above illustrates this result for trees. You can
prove that V - E = 1 for a connected tree by induction on
the number of edges in the tree.

You can then prove the Euler formula for an arbitrary connected
plane graph by just making that graph by adding edges by our type
II move to a tree. Think about this and try some examples.

Logic Problems and Other Problems From Part I.

Problem 2.1.
Proof by Contradiction.
Consider the following proof that the square root of 2 is not
a rational number. At those places where we state an exercise, do
the exercise.

Proof. Suppose that there is a rational number p/q whose square is
equal to 2. We can assume that p/q is in reduced fractional form
and that it is positive. Thus we assume that p and q are positive
integers and that they do not have a common divisor other than 1.

So (p/q)² = 2.
Whence p²/q²= 2.
Whence p² = 2q².
Thus p² is even.
This implies that p is even
[Exercise: Prove that, when p is a natural number, if p² is
even ,then p is even.]
Therefore p = 2r for some natural number r.
Hence (2r)² = 2q² by substitution into p² = 2q².
This is the same as saying 4r² = 2q².
Dividing this equation by 2, we get
2r² = q². Thus q² is even.

But this means that q is even, by the exercise.
Therefore both p and q are even.
This means that p and q have the common factor 2.
But this contradicts our assumption that p and q do not have a
common factor.
We conclude that the assumption that there is rational number
whose square is 2, leads to a contradiction. Since we assume that
mathematics is consistent, this is a proof by contradiction that the
square root of 2 is irrational. Q.E.D.

This proof is a very good example of a proof by contradiction. We
wish to prove P and we start by assuming ~P and find that this
assumption leads to an absurdity.
We conclude from this that ~P cannot be true. But if ~P is false, then
P is true!

The result that the square root of 2 is not rational was a scandal for
the ancient Greek mathematicians, and even today there is a
mystery about this. It means that the decimal expansion of the
square root of two does not have a periodic pattern, and to know
the square root of two fully as a decimal you would have to know
infinitely many terms of its expansion.

[Exercise: Prove that there is no rational number whose
square is equal to 3.]
Remark on the above exercise. You willl need to prove that
3 divides p² implies that 3 divides p. In order to do this,
note that the natural numbers fall into three disjoint
classes:

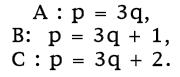
A is the class of all numbers that are divisible by 3.
B is the class of all numbers that leave a remainder of 1
upon division by 3.
C is the class of all numbers that leave a remainder of 2
upon division by 3.

You can show that p² is of type A only if p is of type A.
From this it follows that if p² is divisible by 3, then p is
divisible by 3.

Due Monday, March 2, 2009.

Problem 2.2.
From the book.
p. 9: 1.3, 1.4.
p. 19: 2.1,2.3,2.4,2.5.
p. 53: 1,2.

Due Monday, March 2, 2009.

Problem 2.3.
p. 53: 3.

p. 54: 6.
Due Wednesday, March 4, 2009.

Remark on Problem 6 of page 54:
Here you are asked to use only the axioms given on pages
18 and 19. This is a very stringent exercise! Here is an example of
how one can proceed.
We want to prove that a x 0 = 0. Here is the proof.

Proof that a x 0 = 0.
0 = 0 + 0 by (iv)
Hence a x 0 = a x (0 + 0) and
a x (0 + 0) = a x 0 + a x 0 by the distributive law (iii).
Thus a x 0 = a x 0 + a x 0.
Thus
a x 0 + (- (a x 0) ) = (a x 0 + a x 0 ) + (- (a x 0) )
and
(a x 0 + a x 0 ) + (- (a x 0) ) = a x 0 + (a x 0 + (- (a x 0) )
by the associative law (ii).
Thus
a x 0 + (- (a x 0) ) = a x 0 + (a x 0 + (- (a x 0) )
We know that a x 0 + (- (a x 0) ) = 0 by (vi).
Thus
0 = a x 0 + 0.
Since a x 0 + 0 = a x 0 by (iv), we conclude that
0 = a x 0.
QED.

Note that in applying an axiom like "x + 0 = x for any x"
we can put whatever we like in place of x.
Elephants + 0 = Elephants?
Well, not quite anything we like. It has to be about numbers for
these axioms. So we can say
27 + 0 = 27
and we can say
(xy + 2z) + 0 = (xy + 2z).
In justifying our steps in the proof, we have not explicitly
indicated such substitutions.

Problem 2.4. p. 9 - 1.3, 1.4, 1.5

p. 29, 3.1, 3.2, 3.7
Due Monday, March 10, 2009.

Problem 2.5. This problem introduces an interpretation of
logic in terms of switching circuits. This application of
logic to switching circuits is the discovery of
Claude Shannon

The Journal of Symbolic Logic, Vol. 18, No. 4 (Dec., 1953), p. 347
and forms the basis for the design of computers to this
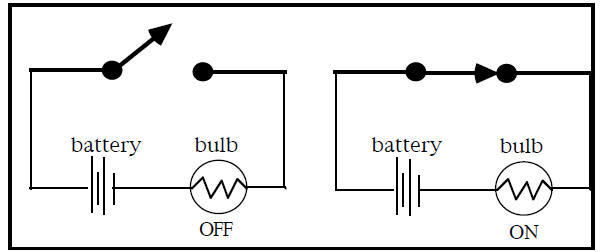
day. Here is an abstract switch:

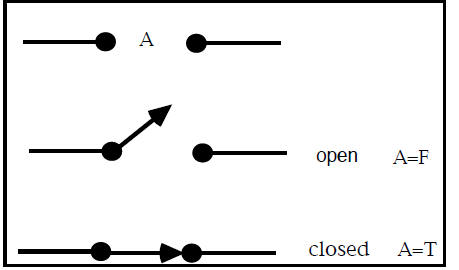
A signal can go from left to right through the switch when
it is closed, and no signal can go through when the switch
is open. We choose to designate a switch by a label such as
A above and we let A = T correspond to the closed switch
position (T for "transmit" if you like!) and we let A = F
when the switch is in the open position (F = ~ T = not
transmit).

The position of a switch can control a device such as a
lamp.

Two basic ways to put switches together are Series and
Parallel Connection:

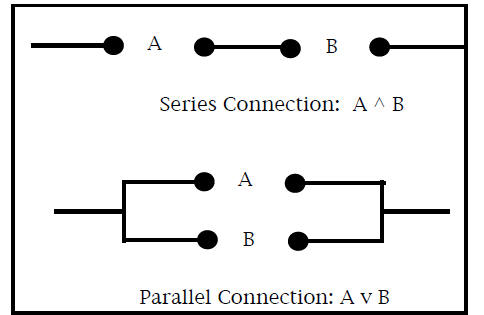
As you can see, the only way for a signal to get from left
to right in the series connection of A and B is if both A and
B are T (closed). Thus the series connection corresponds to
A and B which we write in logic notation as A ^ B.
Similarly, the only way for a signal to get from left to right
in a parallel connection is if one of A or B is closed. Hence
this corresponds to A or B, which we write as A v B.
Thus our two basic logical operations are mirrored in the
behaviour of networks that carry signals.

What about negation? An example will show you how we
handle this. What we do is, we allow multiple appearances
of a given label or its negation. We will write either
~A or A' for the negation of A. Here we will use A' ok?

Then in the mutiple appearances, all A's will be either
closed or open and if you have A' and A is closed, then A'
will be open. If A is open then A' will be closed.
Look at this example:

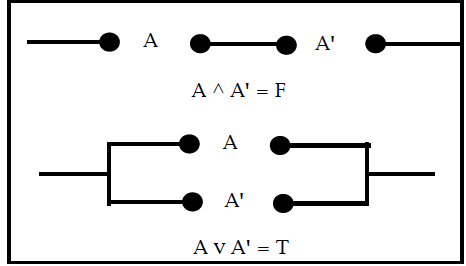
Each of these circuits has an A and an A'. In the series
connection, this means that one switch is always open and
so the value of the whole circuit is the same as a simple
open circuit. On the other hand in the parallel connection
of A with A' either one line will transmit, or the other line
will transmit. So the circuit as a whole behaves like a
single switch that is closed. Thus we see that the series
connecction corresponds to the identity A ^ A' = F, while
the parallel connection corresponds to the identity
A v A' = T.

Terminology: Since a label A in one of our circuits can
appear in many places we will still refer to A as a 'switch'
even though it may be composed of a number of
elementary switches. In such a multiple switch, if you make
one, there has to be a mechanical way to make sure that all
the different parts of the switch work together. Also these
switching patterns may, in practice, happen in elecronic
circuitry that syncronizes actions at separate locations.
For our purposes, we shall imagine simple mechanical
switching devices.

Problem: Illustrate the two identities (distribution laws in
logic) with the correspoinding switching circuits.

(i) a ^ (b v c) = (a ^ b) v (a ^ c)
(ii) a v (b ^ c) = (a v b) ^ (a v c).

In each case, draw the corresponding circuits and explain
why they have the same signal transmission behaviour.
Due Wednesday, March 11, 2009.

Problem 2. 6. Design a switching circuit with three
switch labels a,b,c such that each of a, b and c individually
control transmission of the signal. That is if the circuit is
open, then changing the state of any one of a,b,c will close
the circuit and if the circuit is closed, then changing the
state of any one of a,b,c will open the circuit.
(We discussed how to do this with in analogous case of two
labels and how it is related to (a ^ b) v (a' ^ b') in class.)

Due Monday, March 16, 2009.
Problem 2.7. p. 72, 6.1, 6.4, 6.5, 6.7.
Due Monday, March 16, 2009.
Problem 2.8. p. 86, 7.6, 7.7.
Due Wednesday, March 18, 2009.

Problem 2.9. Generalize Problem 2. 6. to an arbitrary
number N of switch labels. That is, you would like to be
able to control a single lamp with any one of N switches.
You want to find a design that will work in principle for
(say) a building with N floors, so that you can control the
entrance light from any of the floors. The switch on any
given floor will turn the entrance light on or off. That
switch on a given floor will have two positions just as our
labels have two states T or F. This is a hard problem.
The notes on Logic Circuits should make it accessible to
you. See these notes on the website.
Due Monday, March 30, 2009.

Problem 2.10. p. 99, 8.1, 8.2, 8.3
Due Friday, March 20, 2009.
Problem 2.11. p. 113, 9.1,9.2,9.3,9.4,9.5,9.6.

Due Wednesday, April 1, 2009.
Problem 2.12. p. 115, 2., 3., 6., 8.
Due Friday, April 3, 2009.

Problem 2.13.
(a) page 132 #10.3.
(b) Prove that for all sets x,y,z: If {x.y} = {x,z}, then y = z.
(c) Prove that for all sets a,b,c,d:
If {{a},{a,b}} = {{c},{c,d}}, then a = c and b = d.
Due Wednesday, April 8, 2009.

Cantor's Theorem

In class we covered Cantor's proof that P(X) > X for any set X,
where P(X) is the set of subsets of X.
Here is the gist of the proof:
Suppse F:X ----> P(X) is any mapping of these sets.
Let C = {x in X| x is not in F(x)}.
Then C cannot equal F(z) for any z.
To see this, consider a set F(z).
If z is in F(z) then z is not in C and so C and F(z) are different.
If z is not in F(z) then z is in C and so C and F(z) are different.
Therefore C is not of the form F(z) and so F is not surjective.
We have shown that no mapping F:X ----> P(X) is surjective. Since it
is easy to construct an injection from X to P(X) (e.g. x is sent to {x})
this proves that X < P(X).

Problem 2.14.
(a) Let N_n = {1,2,3,...,n} so that N_n has cardinality n.
We write |X| for the cardinality of a set X. And so write
|N_n| = n. Now, let P(X) denote the set of subseets of a given
set X. Prove by induction on n that P(N_n) has cardinality
2ⁿ. That is, |P(N_n)| = 2ⁿ.

(b) Let X = {a, b, c}. Make an explicit form for P(X).
That is, make an explicit list of all the subsets of X.
Choose a function F: X ----> P(X) (make this quite explicit).
Then apply Cantor's process to F and form the
set C = {x in X | x is not in F(x)}. You should find that
C is not of the form F(z) for any z in X. Discuss.

(c) Consider the collection Aleph of all possible sets whose
members are themselves sets . Sets in Aleph can be infinite
or finite. In a sense, Aleph is "the collection of all sets".
Aleph begins with the empty set { }. Then you get
{ { } }. After that, come things like
{ { }, {{ }}, { { }, {{ }} }, {{{ }}} }.

And there are lots of infinite sets of sets. For example
{{}, {{}}, {{{}}}, {{{{}}}}, ...}. And you can take sets of these.
It grows and grows and whenever you have a element X of
Aleph, you can look inside and see that all the members of
X are themselves sets, and hence members of Aleph. So any
member of Aleph is itself a subset of Aleph.

Any subset of Aleph is a collection of sets and so is also a
member of Aleph. Thus it seems that we have proved that
Aleph = P(Aleph) in contradiction to Cantor's Theorem that
says that the power set of a set is always bigger than the
set. Think about this. This is not exactly a puzzle. It is
really a philosophical and mathematical problem about the
use of the word "all". We will discuss this further in class.

Due Friday, April 10, 2009.

Problem 2.15.
Let X be a finite set and Y another finite set.
Let X^Y denote the intersection of X and Y and let
XvY denote the union of X and Y. Let |X| denote the
cardinality of X. Prove, in your own words, the formula
|XvY| = |X| + |Y| - |X^Y|.

Due Monday, April 13,2009.