Math 104A Homework #5

Pg 110

#1: Determine Ø(120) and Ø(225).

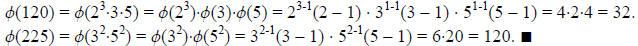
#11: (Schroder) An n-pointed star has n points lying equidistant on a circle joined by n
straight lines. A point cannot be joined to a neighboring point on the circle. We
require that the start be symmetric, that is, the angle between the two lines that meet
at a point is the same for all points. Show that the number of n-pointed stars that can
be drawn with n lines using consecutive strokes without lifting the pen is (Ø(n) –
2)/2; hence a 6-pointed star cannot be drawn with 6 consecutive strokes.

The only valid stars are those that fill every node (all n of them). Once we pick a
distance to go for each line, the only stars that work are those that cycle around
back to our starting point after hitting every other node. If the distance we choose to
go is not relatively prime to n, then we will fail to reach every node and end up back
at our starting point too soon.

And so, the problem essentially boils down to finding how many numbers have an
inverse mod n. By Euler’s Phi-function, we see that there are Ø(n) numbers
relatively prime to n.

This is all fine and dandy, but one of the stipulations for the creation of a star is that
a point cannot be joined to a neighboring point on the circle. Thus, we cannot use 1
and n – 1 as distances to travel, since they would be neighboring our initial point.
Notice that 1 and n – 1 are among the list of those counted in Ø(n). Thus, we really
have Ø(n) – 2 numbers with inverses that we can use to create stars from.

This, however, counts too many stars. By the above method, going around the star
to the right and to the left create different stars, though the results will be the same
by symmetry. Consequently, we need to divide our total by 2 to remove all of the
duplications.

And so, we see that the number of n-pointed stars that can be drawn with n lines
using consecutive strokes without lifting the pen is (Ø(n) – 2)/2.

Since Ø(6) – 2 = 2 – 2 = 0, we see that there is no way to draw a 6-pointed start with
6 consecutive strokes. ■

Pg 116

#1: Use Euler’s Theorem to compute the following quantities.

(a) 3³⁴⁰ mod 341

First we know that since the digits of 341 do not sum to a multiple of 3, then
(3, 341) = 1. Notice that 341 = 31·11. And so, we see that Ø(341) = Ø(11·31) =


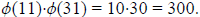
By Euler’s Theorem, then we see that 3³⁰⁰ ≡ 1 (mod 341). And so, that means that
3³⁴⁰ ≡ 3⁴⁰ mod 341.

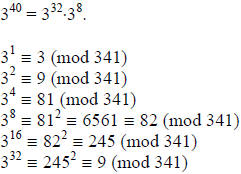
We see that 3⁴⁰ ≡ 9·82 ≡ 56 (mod 341). And so, 3³⁴⁰ ≡ 56 (mod 341). ■

(b) 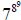mod 100.

Since 7 and 100 are relatively prime, by Euler’s Theorem, we know that
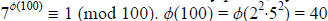. The question becomes, though,
what is the remainder when 8⁹ is divided by 40? To compute that, we set up
another congruence, namely 8⁹ (mod 40).

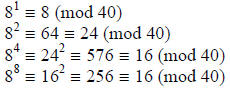
And so, 8⁹ ≡ 16·8 ≡ 128 ≡ 8 (mod 40). Thus, the original question, 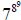mod 100,
boils down to 7⁸ mod 100.

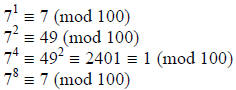
And so, we see that 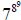≡ 7 (mod 100). ■

#3: Use Euler’s Theorem (and the Chinese Remainder Theorem) to show that
n¹² ≡ 1 (mod 72) for all (n, 72) = 1.

We begin by breaking 72 into two factors, namely 8 and 9. Notice that by Euler’s
Theorem, we have that 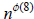≡ 1 (mod 8) and 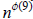≡ 1 (mod 9). Well, Ø(8) = 4 and
Ø(9) = 6, so we have n⁴ ≡ 1 (mod 8) and n⁶ ≡ 1 (mod 9).

Notice, though, that since n⁴ ≡ 1 (mod 8), then n^4·3 = n¹² ≡ 1 (mod 8). Likewise, we
observe that since n⁶ ≡ 1 (mod 9), then it follows that n^6·2 = n¹² ≡ 1 (mod 9).

By the Chinese Remainder Theorem, we see that n¹² ≡ 1 (mod 72) (since the two
numbers n¹² and 1 are the same modulo 8 and 9). ■

#Extra Credit: Let (m, n) = 1 and (a, mn) = 1. Show that .

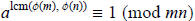If (a, mn) = 1, then that implies that (a, m) = 1 and (a, n) = 1. By Euler’s Theorem, we
have that 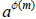≡ 1 (mod m) and 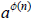≡ 1 (mod n), since (a, m) = (a, n) = 1.

Claim: 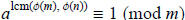  and, by symmetry, .

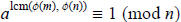Proof: By the definition of least common multiple, we see that
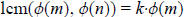for some integer k and also that
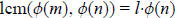for some integer l.

Since 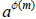≡ 1 (mod m), then we have the following:

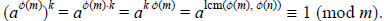
Likewise, we see that 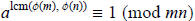, proving the claim.

Now, we have 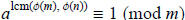and 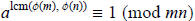. By the Chinese
Remainder Theorem, we see that 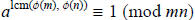(because the two
numbers 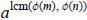and 1 are the same modulo m and n). ■

Pg 119

#1: Find the four solutions of x⁴ ≡ 1 (mod 13).

The text tells us that 1 and -1 (12) are solutions. There are still two more, though.
Simple calculations reveal that 5 and -5 (8) are also solutions. So, the four solutions
of are x ≡ 1 (mod 13), x ≡ 5 (mod 13), x ≡ 8 (mod 13), and x ≡ 12 (mod 13). ■

#5: Let p be an odd prime and let

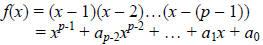
(a) Show that x^p-1 – 1 ≡ f(x) (mod p).

By Corollary 4.4.3, since (p – 1) | (p – 1), then we see that the congruence
x^p-1 – 1 ≡ 0 (mod p) has exactly p – 1 solutions. We need to show that all of the
solutions are distinct, though.

Case (i): x ≡ 0 (mod p). Notice that f(0) = (0 – 1)(0 – 2)…(0 – (p – 1))
= (-1)^p-1(p – 1)! = (p – 1)! Also, (0)^p-1 – 1 ≡ -1 (mod p).
And so, f(0) ≡ -1 (mod p).

Case (ii): x ≡ i (mod p), 1 ≤ i ≤ p – 1. By Fermat’s Little Theorem, we see that
x^p-1 ≡ 1 (mod p), i.e. x^p-1 – 1 ≡ 0 (mod p). Notice also that
f(i) ≡ 0 (mod p) since f(i) = (i – 1)(i – 2)…(i – i)…(i – (p – 1)) = 0.
Thus, f(i) ≡ i^p-1 – 1. ■

(b) Compare the coefficients of x on both sides and conclude that ≡ -1 (mod p) and
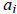≡ 0 (mod p) for 1 ≤ i ≤ p – 2.

Look at f(p) (mod p). Plugging in p for x, we see that f(p) = in the bottom
equation and in the top equation, it will be equal to (p – 1)(p – 2)…1 = (p – 1)!
Since p is an odd prime, by Wilson’s Theorem, we see that (p – 1)! ≡ -1 (mod p).

From (a), we see that x^p-1 – 1 ≡ f(x) (mod p). We just saw that ≡ -1 (mod p),
and so that means that for (a) to hold, 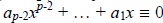(mod p). Since x
is arbitrary, we see that 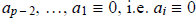(mod p) for 1 ≤ i ≤ p – 2. ■

(c) Show that 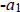is the numerator of 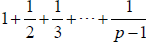. Since f(p) ≡ -1 (mod p)
and 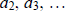are divisible by p, show that is divisible by p². This result is
known as Wolstenholme’s Theorem.

Notice that a1 is the coefficient in front of the x term. 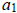= 1·(-2)·…·(-(p – 1)) +
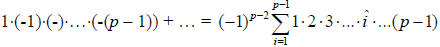, where 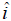means i is
not included.

Since p is odd, .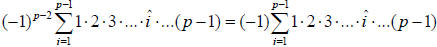
The numerator of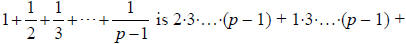
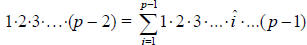, which is the negative of above, and so
we have shown that the two are equal.

In (b), we showed that f(p) = (p – 1)! = 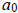. This gives us the following equation:



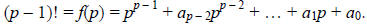
But, 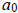= (p – 1)!, so we actually have the following:



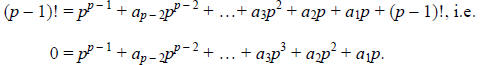
Dividing both sides by p, we have the following:



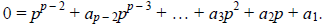
Let’s examine this equation mod p². Notice that the first p – 3 terms are all
congruent to 0 (mod p²), and so we are left with the following equation:

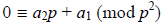. Recall from (b), we showed that 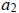≡ 0 (mod p), i.e.
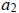= kp for some integer k. That means that we have:

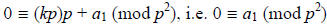, i.e. 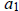is divisible by p². ■