Intermediate Algebra Course Syllabus

COURSE DESIGNATION
MAT 099, Intermediate Algebra. MAT 099 serves as the prerequisite to MAT 103 or MAT 104 for students who do
not have two years credit of high school algebra. The Mississippi Board of State Institutions of Higher Learning (IHL)
requires that all entering freshmen with an ACT math subscore of 16 or below take MAT 099 during their first semester
of enrollment at an IHL university. Students are required to maintain continuous enrollment in MAT 099 until a passing
grade is obtained. Additionally, students required to take MAT 099 will not be allowed to withdraw from the class, nor
will they be allowed to enroll in any additional math courses until a passing grade has been earned in the MAT 099. This
course does not satisfy any degree requirements; however, a failing grade in MAT 099 will be included when computing
the student’s GPA with regards to full-time status, academic and financial aid, probation or suspension. Any student
receiving an F in MAT 099 will automatically be registered for MAT 099 for the next regular term of classes. If a student
who has preregistered for MAT 103 or MAT 104 and fails MAT 099, the student will be dropped from the class roll of
the upper level math and reinstated in MAT 099.

TEXT
D. Franklin Wright, Intermediate Algebra. Fifth Edition. Hawkes Publishing 2004.

General Course Objectives
Upon completion of the course, the student will be able to:
1. Find the sum, difference, product, and quotient of any two real numbers.
2. Evaluate, simplify and perform operations with algebraic expressions.
3. Solve linear, quadratic and miscellaneous equations and their applications.
4. Solve linear inequalities.
5. Factor and perform operations with polynomials.
6. Simplify radical expressions and solve equations involving radicals.
7. Find the slope and equations of lines and sketch their graphs.

TUTORING SERVICE
Free tutoring will be available in the Mathematics Department for students who need help outside of class. Hours when
tutors are available will be given to the students and posted on the door of the tutor room, Walters 278.
Help is also available in the Academic Support Lab, room 311 of the H. L. Nowell Union Building from 11:00 am
to 5:00 p.m. daily. There are 10 computers with headphones to accommodate the Hawkes Learning Systems software
program. See or call Diane Blansett, director, at 846-4654.

CLASS ATTENDANCE
Prompt and regular attendance is necessary for success in this course. To receive credit in this course, you must
attend a minimum number of the class meetings. Classes meeting three times per week will be allowed a total of 6
absences, excused and unexcused. If you exceed the allowable number of absences, a grade of “F” will be
assigned as the final grade in the course. To be counted present, you must arrive on time for the class and remain in
class the entire time. When you are tardy for class, it is your responsibility to request that I change the recorded absence
to a tardy. This must be done on the day the tardy occurs. A maximum of 3 tardies will be allowed without
consequences. Each additional tardy will be recorded as an unexcused absence. Each student must spend an hour
in the computer lab each week as part of this course.

The comprehensive Final Exam for this course is scheduled for December 8, 2009 at 8:00 am. You must take the final
exam to pass this class.

OFFICE HOURS

Monday	Tuesday	Wednesday	Thursday	Friday
07:30 – 08:00	07:30 – 08:00	07:30 – 08:00	07:30 – 08:00	07:30 – 08:00
09:00 – 10:00	09:30 – 10:45	09:00 – 10:00	09:30 – 10:45	09:00 – 10:00
11:00 – 12:00		11:00 – 12:00		11:00 – 12:00

Other Times by Appointment

GRADING AND EVALUATION
1. Unannounced quizzes may be given throughout the semester (based on homework assignments).
2. Homework will count as 20% of your final grade. Homework (to be done on the computer using Hawkes
Learning Systems software) must be done by the due date to get full credit.
Late homework penalties will be assessed as follows:
• 10% for homework 1days late;
• 20% for homework 2-3 days late;
• 50% for homework 4-7 days late;
• 100% for homework more than 7 days late.
3. Four scheduled tests will be given during the semester.

Your final grade will be the average of: the homework grade; the 3 best scheduled test grades; and the final exam
(all equally weighted). Credit for computer lab attendance will be included in the homework grade.

There will be No Extra Credit or “make-up” work to improve your grade.

Grades will be assigned according to the following scale:
A ( 93 – 100 )
B ( 85 – 92 )
C ( 77 – 84 )
D ( 70 – 76 )
F ( Below 70 )

Cheating and plagiarism are not tolerated. If it is established that a violation has occurred, the instructor may
determine the penalty, or he/she may report the offense to the department chair and dean of the school. The usual penalty
involves a grade of zero on the test, examination or paper in question.

CLASSROOM POLICIES AND MAKE-UP TESTS
1. Do NOT go to SLEEP in this CLASS!!!
2. Do not use tobacco or eat in the classroom.
3. Do come to class on time and be prepared to begin class at the scheduled time.
4. Do not ask to leave class early. Schedule all appointments at times that do not conflict with class time.
5. Cell Phones and Pagers must be turned off during class. Cell Phones may not be used as calculators.
6. Calculator use is permitted during all classes and tests.
7. Scheduled tests will be announced at least a week prior to the actual test date.
8. Be sure to show all work on tests. No partial credit will be given if the work is not shown in detail.
“Answers only” will not be accepted.
9. Come to my office for help during scheduled office hours. No appointment is necessary. It is extremely
important that you understand the material and are able to complete the homework assignments for each
class prior to the next class. Tutoring is also available in Walters 278.
10. You must expect to practice assigned problems until you understand them.
11. Make-up tests will be given only to those students presenting a written excuse, acceptable by the university.
Any absence from scheduled work must be covered by a written excuse by the Vice President for Academic
Affairs, the Student Health Service, or a doctor before the student is allowed to make up that work. All makeup
must be completed within three days of the originally scheduled test.
12. Buy a scientific calculator or graphing calculator early in the semester and learn how to use it. Do not
expect me to know how to use your calculator without the manual. Please do not ask to borrow a
calculator from me or one of your classmates on test day since rarely do two calculators operate exactly the
same. BRING YOUR CALCULATOR TO CLASS EVERY DAY.

IMPORTANT DATES
August 25, 2009 is the last day that a course may be added to your schedule; this includes changes from one section to
another within the same course. If you plan to audit this course, you must make the change by August 28, 2009.
Students who remain in the course after August 31, 2009, and who elect to drop the course will receive a grade of W if
passing or F if failing the course at the time of the drop. The withdrawal process in not complete until the drop slip has
been signed by all designated parties and the completed form has been turned in to the Registrar’s office. The last day to
drop a class is December 4, 2009.
The comprehensive Final Exam for this course is scheduled for December 8, 2009 at 8:00 am. You must take the
exam on the day it is given.

Labor Day Holiday	September 7, 2009
Fall Break	October 15 –26, 2009
Thanksgiving Holidays	November 23 - 27, 2009

Practice Problems for MAT 099 Intermediate Algebra

Section 1.1 (Properties of Real Numbers)
p. 14: #’s 1-11 odd, 27-33 odd, 63-65, 69
Section 1.2 (Operations with Real Numbers)
p. 29: #’s 1, 3, 5, 7, 9-13, 17-19, 21, 22, 23, 25, 29, 30, 31, 33, 41, 45, 46, 48-50, 57, 59, 67, 69, 71, 73, 75, 77
Section 1.3 (First-Degree/Linear Equations and Absolute Value Equations)
p. 41: #’s 1-35 odd, 41, 43, 49, 51
Section 1.4 (Evaluating and Solving Formulas)
p. 48: #’s 1-15 odd, 26, 30
Section 1.5 (Applications)
p. 58: #’s 1, 3, 7, 9, 11, 16,41
Section 1.6 (Linear Inequalities and Absolute Value Inequalities)
p. 73: #’s 1, 3, 5, 7, 13, 15, 21, 23, 31, 33, 46, 47, 48, 51a
Section 1.7 (Properties of Exponents)
p. 82: #’s 1-13 odd, 17, 19, 24, 26, 29, 33-41 odd, 49, 53, 69
Section 1.8 (More on Exponents and Scientific Notation)
p. 91: #’s 1-7 odd, 8, 9, 15, 17, 20, 21
Section 2.1 (Cartesian Coordinate System and Straight Lines: Ax + By = C)
p. 110: #’s 1, 5, 9, 17, 35-38. 17-22 => Find the intercepts and graph only.
Section 2.2 (Slope-intercept Form: y = mx + b )
p. 121: #’s 1, 2, 4, 6, 9, 13, 17-19, 21, 25, 27, 43, 44, 48, 49-51
Section 2.3 (Point-slope Form: )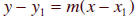
p. 135: #’s 1-7odd, 8, 17, 19, 21, 23, 24-36 even, 48-51
Section 2.4 (Introduction to Functions)
p. 153: #’s 1, 3, 5, 9, 15, 17, 18, 20, 21, 23, 24, 31-34
Section 4.1 (Addition and Subtraction of Polynomials)
p. 259: #’s 1, 3, 13-23odd, 27, 31, 37, 38, 41
Section 4.2 (Multiplication of Polynomials)
p. 268: #’s 1-13 odd, 17-29 odd, 49, 52, 63
Section 4.3 (Division with Polynomials and Synthetic Division)
p. 279: #’s 1, 3, 7, 11
Section 4.4 (Introduction to Factoring)
p. 292: #’s 1, 3, 5, 9, 11-21 odd, 24, 25, 27, 28, 41, 44
Section 4.5 (Introduction to Factoring)
p. 299: #’s 1, 3, 6-9, 11, 14, 17, 33-39 odd
Section 4.6 (Polynomial Equations and Applications)
p. 311: #’s 1, 3, 7, 11, 14, 15, 17-29 odd, 53-55, 59, 60
Section 5.1 (Multiplication and Division of Rational Expressions)
p. 338: #’s 11-19, 24, 26, 35, 37, 44
Section 5.2 (Adding and Subtracting of Rational Expressions)
p. 348: #’s 1, 3, 8, 15
Section 5.4 (Equations and Inequalities with Rational Expressions)
p. 348: #’s 1, 3, 5, 7, 21
Section 6.1 (Roots Radicals and Complex Numbers)
p. 410: #’s 11, 12, 16, 21
Section 6.3 (Arithmetic with Radicals)
p. 429: #’s 1, 3, 4, 7, 9, 16, 11, 22
Section 7.1 (Quadratic Equations: Completing the Square)
p. 476: #’s 1, 3, 5, 9-19 odd, 27, 29, 33, 35, 37, 40, 41
Section 7.2 (Quadratic Equations: The Quadratic Formula)
p. 484: #’s 2, 4, 6, 8, 25, 27, 28, 29, 31, 33, 41, 43-45, 52
Section 8.1 (Quadratic Functions: Parabolas)
p. 527: #’s 1, 2, 9, 13, 16, 25 – 28, 31, 33, 35