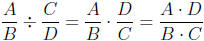Dividing Fractions
0.1 Dividing Fractions
In this section, we will discuss the two interpretations of division for
fractions,
and we will see why the standard "invert and multiply" procedure for dividing
fractions gives answers to fraction division problems that agree with what
we expect from the meaning of division.
The Two Interpretations of Division for Fractions
Let's review the meaning of division for whole numbers, and see how to
interpret division for fractions.
The "how many groups?" interpretation
With the "how many groups?" interpretation of division, 12 ÷ 3 means the
number of groups we can make when we divide 12 objects into groups with
3 objects in each group. In other words, 12 ÷ 3 tells us how many groups of
3 we can make from 12.
Similarly, with the "how many groups?" interpretation of division,
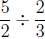
means the number of groups we can make when we divide
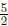 of an object
of an object
into groups with 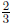 of an object in each group.
In other words,
of an object in each group.
In other words, 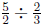 tells us
tells us
how many groups of 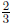 we can make from
we can make from
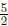 . For example, suppose you are
. For example, suppose you are
making popcorn balls and each popcorn ball requires
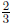 of a cup of popcorn.
of a cup of popcorn.
If you have 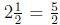 of a cup of popcorn, then how
many popcorn balls can
of a cup of popcorn, then how
many popcorn balls can
you make? In this case you want to divide 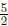 of
a cup of popcorn into groups
of
a cup of popcorn into groups
(balls) with
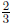 of a cup of popcorn in each
group. According to the "how
of a cup of popcorn in each
group. According to the "how
many groups?" interpretation of division, you can make
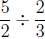
popcorn balls.
The "how many in one (each) group?" interpretation
With the "how many in each group?" interpretation of division, 12 ÷ 3 means
the number of objects in each group when we distribute 12 objects equally
among 3 groups. In other words, 12 ÷3 is the number of objects in one group
if we use 12 objects to evenly fill 3 groups. When we work with fractions, it
often helps to think of "how many in each group?" division story problems as
asking "how many are in one whole group?", and it helps to think of filling
groups or part of a group. So in the context of fractions, we will usually
refer to the "how many in each group?" interpretation as "how many in one
group?".
With the "how many in one group?" interpretation of division,
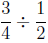
is the number of objects in one group when we distribute
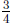 of an object
of an object
equally among  of a group. A clearer way to
say this is:
of a group. A clearer way to
say this is: 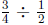 is the
is the
number of objects (or fraction of an object) in one whole group when
![]() of
of
an object fills  of a group. For example,
suppose you pour
of a group. For example,
suppose you pour ![]() of a
pint of
of a
pint of
blueberries into a container and this fills  of the container. How many pints
of the container. How many pints
of blueberries will it take to fill the whole container? In this case,
![]() of a
of a
pint of blueberries fills (i.e., is distributed equally among)
 of a group (a
of a group (a
container). So according to the "how many in one group?" interpretation
of division, the number of pints of blueberries in one whole group (one full
container) is
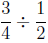
One way to better understand fraction division story
problems is to think
about replacing the fractions in the problem with whole numbers. For example,
if you have 3 pints of blueberries and they fill 2 containers, then how
many pints of blueberries are in each container? We solve this problem by
dividing 3 ÷ 2, according to the "how many in each group?" interpretation.
Therefore if we replace the 3 pints with
![]() of a pint, and the 2
containers with
of a pint, and the 2
containers with
 of a container, we solve the problem in the
same way as before: 3 ÷ 2 now
of a container, we solve the problem in the
same way as before: 3 ÷ 2 now
becomes 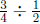 .
.
Here is another way to think about the problem. Because
 of the container
of the container
is filled, and because this amount is
![]() of a pint, therefore
of a pint, therefore
 of the
of the
number of pints in a full container is
![]() of a pint. In other
words:
of a pint. In other
words:
![]() ×number of pints in
full container =
×number of pints in
full container = ![]()
Therefore
number of pints in full container =
![]()
Dividing by ![]() Versus
Dividing in
Versus
Dividing in ![]()
In mathematics, language is used much more precisely and carefully than in
everyday conversation. This is one source of difficulty in learning mathematics.
For example, consider the two phrases:
dividing by ![]() ,
,
dividing in ![]() .
.
You may feel that these two phrases mean the same thing, however,
mathematically,
they do not. To divide a number, say 5, by
![]() means to calculate
means to calculate
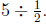 Remember that we read A÷ B as A divided by
B. We would divide
Remember that we read A÷ B as A divided by
B. We would divide
5 by ![]() if we
wanted to know how many half cups of our are in 5 cups of
if we
wanted to know how many half cups of our are in 5 cups of
our, for example. (Notice that there are 10 half-cups of our in 5 cups of
our, not 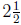 .)
.)
On the other hand, to divide a number in half means to find half of that
number. So to divide 5 in half means to find
![]() of 5. One half of 5
means
of 5. One half of 5
means
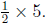 So dividing in
So dividing in
![]() is the same as
dividing by 2.
is the same as
dividing by 2.
The "Invert and Multiply" Procedure for Fraction Di-vision
Although division with fractions can be difficult to interpret, the procedure
for dividing fractions is quite easy. To divide fractions, such as
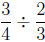 and
and
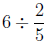
we can use the familiar "invert and multiply" method in
which we invert the
divisor and multiply by it:
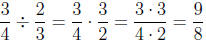
and
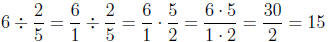
reciprocal
Another way to describe this "invert and multiply" method
for dividing
fractions is in terms of the reciprocal of the divisor. The reciprocal of
a
fraction 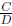 is the fraction
is the fraction
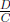 . In order to divide fractions, we should
multiply
. In order to divide fractions, we should
multiply
by the reciprocal of the divisor. So in general,