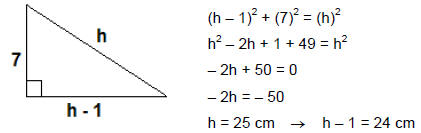Functions, Equations, and Inequalities

2.3 Quadratic Equations, Functions, and Models

I. Definitions of a Quadratic Equation and a Quadratic Function

A quadratic equation in standard form is an equation equivalent to ax² + bx + c = 0 where a, b,
and c are real numbers and a ≠ 0. X-values which make the equation true are called the solutions
or roots of the equation. A quadratic equation can have at most two solutions / roots.

A quadratic function is a function which can be written in the form f(x) = ax² + bx + c where a, b,
and c are real numbers and a ≠ 0. X-values which make f(x) = 0 are called the zeros of the
function. A quadratic function can have at most two zeros.

The real zeros of a function are the first coordinates of the x-intercepts of the graph of the
function. The graph of a quadratic function can have at most two x-intercepts.

II. Equation-Solving Principles

The Principle of Zero Products:	If a·b = 0, then a = 0, b = 0, or both = 0. If a = 0, b = 0, or both = 0, then a·b = 0.
The Principle of Square Roots:	If x2 = k, then 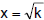or .
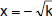The Quadratic Formula:	If ax2 + bx + c = 0, then .

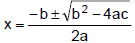III. Five Methods of Solving Quadratic Equations

A. Solving Quadratic Equations by Factoring and Using the Zero Products Principle

1. Put equation in standard form. Factor out the greatest common factor (GCF).

2. Look for patterns such as a difference of squares, x² – y² = (x – y)·(x + y) or
a perfect square trinomial, x² + 2xy + y² = (x + y)² or x² – 2xy + y² = (x – y)².

3. If there is no pattern, factor by trial and error or factor by grouping.
If you don’t remember how to factor, you should review section R4.

4. Once you have factored, set each factor equal to zero and solve.

Example 1

Solve the equation 12x³ – 8x = –10x² by factoring. (like # 17 & 18 pg. 213)

12x³ + 10x² – 8x = 0

2x (6x² + 5x – 4) = 0

Factoring 6x² + 5x – 4:

6 × –4 = –24 → We are looking for two factors of –24 that add up to 5.

Pairs of Factors of –24	Sums of Factors

The pair that we are looking for is –3, 8. We can now rewrite 5x as 8x – 3x. And then
factor by grouping.

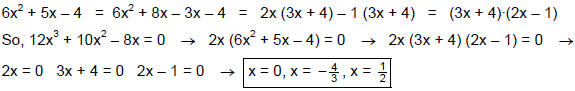
B. Solving Quadratic Equations by Using the Square Roots Principle

Note: This is the best method to use if the quadratic equation does not have an x term.
It is also called extracting the roots.

1. Isolate the squared term which contains the variable.

2. Take the square root of both sides. Be sure you put ± in front of the radical on the
right side.

3. Solve for the variable.

Example 2

Solve 4x² + 12 = 0. (# 12 pg. 213)



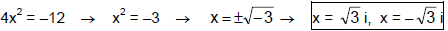
C. Solving Quadratic Equations by Using the Quadratic Formula

1. Write the equation in standard form.

2. Identify a (the coefficient of the squared term), b (the coefficient of the 1st degree
term) and c (the constant).

3. Plug a, b, & c into the Quadratic Formula.

4. Solve for x. Write the solutions in simplified form.

Example 3

Solve 5x² + 3x = 1 by using the quadratic formula. (# 50 pg. 214)



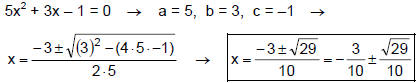
D. Solving Quadratic Equations by Completing the Square

1. Write the equation in standard form. If a ≠ 1, divide every term by a.

2. Subtract the constant from both sides of the equation.
3. Add 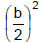to both sides of the equation. Remember, b is the coefficient of the
constant term.
4. Rewrite the left side as 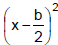. Simplify the right side.

5. Solve by extracting the roots.

Example 4

Solve 2x² – 5x – 3 = 0 by completing the square. (# 34 pg. 213)


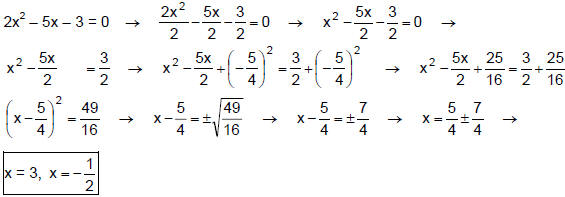
E. Solving Quadratic Equations Graphically

1. Put the equation in standard form, ax² + bx + c = 0

2. Enter ax² + bx + c at .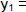

3. Graph the equation and adjust the window so that you can see all of the x-intercepts.

4. Use 2nd Trace 2 (root or zero) to find all of the zeros.

Note: This same basic process can be used to solve any equation with real solutions.
You can also solve an equation graphically by entering the left side as 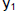, the right side
as 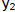, and then using 2^nd Trace 5 (Intersect) to find the x-values of the points of
intersection.

Example 5

Solve 3x² + 5x = 3 graphically. Round solutions to 3 decimal places. (# 116 pg. 215)



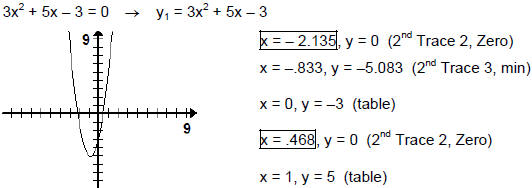
III Solving Equations which are Quadratic in Form ax²ⁿ + bxⁿ + c = 0

1. Rewrite the equation as a quadratic by substituting u for the expression following b.
i.e., Let u = xⁿ, then rewrite ax²ⁿ + bxⁿ + c = 0 as au² + bu + c = 0.

2. Solve for u.

3. Back substitute u values in to xⁿ = u and solve for x.

Example 6

Solve x⁴ + 3x² = 10. (# 79 pg. 214

x⁴ + 3x² – 10 = 0 Let u = x². Then the equation becomes u² + 3u – 10 = 0

u² + 3u – 10 = 0 → (u + 5) (u – 2) = 0 → u + 5 = 0, u – 2 = 0 →

u = –5, u = 2 Replace u with x²→x²= –5, x² = 2 →

IV. Useful Formulas for Solving Quadratic Applications

Pythagorean Theorem: For a right triangle with legs a & b and hypotenuse c, a² + b² = c².

Area of a Rectangle: A = L·W

Perimeter of a Standard Rectangle: P = 2L + 2W

Volume of a Box: V = L · W · H

Example 7

The director of the Glen Island Zoo wants to use 170 m of fencing to enclose a
petting area of 1750 m². Find the dimensions of the petting area. (#104 pg. 215)

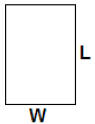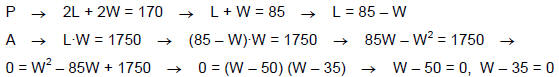W = 50 m or 35 m → If W = 35 m, then L = 85 – 35 = 50 m. → 35 m by 50 m N.B.: We usually let the smaller dimension be the width and the larger dimension be the length

Example 8

One leg of a right triangle is 7 cm. The other leg is 1 cm less than the hypotenuse.
Find the length of the hypotenuse and the length of the second leg. (like # 98 pg. 214)