THE SIXTY-NINTH ANNUAL WILLIAM LOWELL PUTNAM EXAMINATION
Problem A5
Let n ≥ 3 be an integer. Let f(x) and g(x) be polynomials with real coefficients
such that the
points 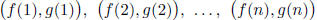 in R2 are the vertices of
a regular n-gon in
in R2 are the vertices of
a regular n-gon in
counterclockwise order. Prove that at least one of f(x) and g(x) has degree
greater than or equal
to n - 1.
Solution: Consider the polynomial p(x) = f(x) + ig(x), whose degree is
the maximum of the
degrees of f and g and which maps { 1, 2, ... , n} onto the vertices of this
polygon. With a suitable
choice of a complex constant 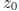 (equal to the
center of the polygon), and a nonzero complex number
(equal to the
center of the polygon), and a nonzero complex number
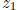 , we can replace this polynomial with the
polynomial
, we can replace this polynomial with the
polynomial
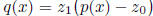 , whose degree is the
, whose degree is the
same as that of p(x), that is, equal to the maximum of the degrees of f(x) and
g(x), and which
maps 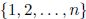 to
to 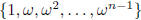 ,
in that order, where
,
in that order, where
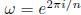 . We need to show that
. We need to show that
the degree of q(x) is at least n - 1.
Suppose not, that is, suppose 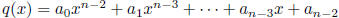 . The
coefficients
. The
coefficients
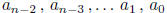 satisfy the following linear system of n - 1
equations:
satisfy the following linear system of n - 1
equations:
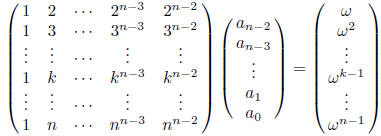
Now this system has a Vandermonde matrix, and can
therefore be solved for the coefficients
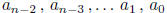 , which are uniquely determined. (The
determinant of the Vandermonde
, which are uniquely determined. (The
determinant of the Vandermonde
matrix is 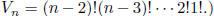 The point of this analysis
is that there is one and only one
The point of this analysis
is that there is one and only one
polynomial of degree at most n - 2 that maps 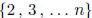 onto
onto  in that order.
in that order.
But that polynomial is obviously
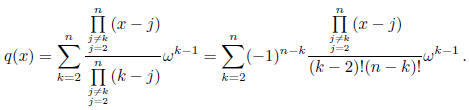
What we need to show is that q(1) cannot be 1. But that is obvious, since
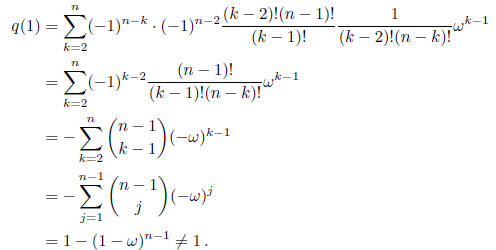
Problem A6
Prove that there exists a constant c > 0 such that in every nontrivial finite
group G there exists
a sequence of length at most 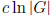 with the
property that each element of G equals the product
with the
property that each element of G equals the product
of some subsequence. (The elements of G in the sequence are not required to be
distinct. A
subsequence of a sequence is obtained by selecting some of the terms, not
necessarily consecutive,
without reordering them, for example, 4, 4, 2 is a subsequence of 2, 4, 6, 4, 2,
but 2, 2, 4 is not.)
Solution: If we make the convention that the identity element e can be
represented as an empty
product, the constant c can be taken equal to 6. With this convention, the
restriction to non-trivial
groups can be removed also, since a string of 0 elements will represent the only
element in the
trivial group feg, and we'll certainly have 0 ≤ 6 ln(1) = 0.
Let G be any finite group, and let a any element of G different from the
identity. Since G is
finite, a has finite order, say k ≥ 2, that is, ak = e. Let r be the
unique positive integer such that
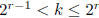 . Then each of the elements a j ,
0 ≤ j < k (where a0 = e) has a unique representation
. Then each of the elements a j ,
0 ≤ j < k (where a0 = e) has a unique representation
as a product of the elements 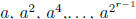 , since each
integer j with 1 ≤ j < k has a unique
, since each
integer j with 1 ≤ j < k has a unique
binary representation as a sum of powers 2i with 0 ≤ i ≤ r - 1. Thus
we can now represent the
k distinct elements a j , 0 ≤ j < k, as products of the r elements
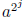 , 0 ≤ j ≤ r - 1. Notice that
, 0 ≤ j ≤ r - 1. Notice that
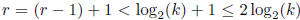 . Thus, at this stage, we can represent k
elements of the
. Thus, at this stage, we can represent k
elements of the
group using a string of at most 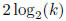 elements,
taken from the sequence
elements,
taken from the sequence
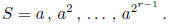
If G consists only of the cyclic group H generated by a,
we are done, and indeed c = 3 > 2/ ln(2)
will suffice in this case. If H ≠ G, let b be an element not in H, and let l ≥ 2
be the smallest
positive integer such that 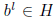 . Just as above,
we know that any power b
j , 0 ≤ j < l, can be
. Just as above,
we know that any power b
j , 0 ≤ j < l, can be
represented as a product of the s powers 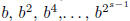 ,
where
,
where
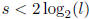 . We now form the
. We now form the
sequence
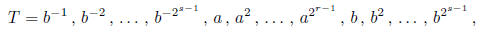
which contains 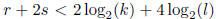 elements. The set K of products of subsequences of
elements. The set K of products of subsequences of
T consists of the elements 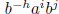 for which 0 ≤ h <
l, 0 ≤ i < k, and 0 ≤ j < l. At least kl
for which 0 ≤ h <
l, 0 ≤ i < k, and 0 ≤ j < l. At least kl
of these are distinct, namely the elements 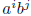 .
For if
.
For if
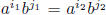 with
with 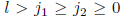 ,
then
,
then
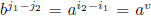 for some v with 0 ≤ v < k. Since
for some v with 0 ≤ v < k. Since
 , this means
, this means 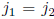 and
and
hence 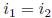
If G = K, we are now done, since that means
![]() ≥ kl, and we have
represented every element
≥ kl, and we have
represented every element
of the group by a product taken from the sequence T, which consists of at most
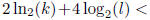
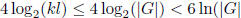 ) elements.
) elements.
If G ≠ K, let d ∈ G\K, and let m ≥ 2 be the smallest positive integer such that
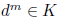 . We
. We
then form the sequence
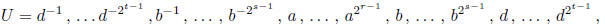
where 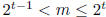 , so that
, so that
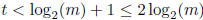 .
.
The products of subsequences of the sequence U form a set L of elements
containing all products
of the form
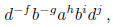
where 0 ≤ f < m, 0 ≤ g < l, 0 ≤ h < k, 0 ≤ i < l, and 0 ≤
j < m. At least klm of these are
distinct, namely the products 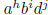 . For if
. For if
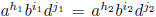 , with
, with 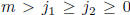 ,
then
,
then
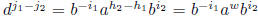 for some w with 0 ≤ w < k. Since
for some w with 0 ≤ w < k. Since
 , it follows
, it follows
that  , and then, by what was proved about the
set K above, that
, and then, by what was proved about the
set K above, that
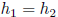 and
and 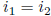 .
.
If L = G, we are now done, having represented every element of G as a product
taken from
a sequence containing fewer than 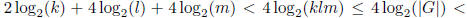
6 ln(![]() ) elements.
) elements.
It is now clear that this process can be continued until the group G is entirely
exhausted.

