THE SIXTY-NINTH ANNUAL WILLIAM LOWELL PUTNAM EXAMINATION

Remark: For all solvable groups G, the constant 6 can be reduced to 3. We already saw this
above, with the cyclic group H. Now let G be a solvable group. Either G is a simple group and
hence cyclic, or it has a non-trivial normal subgroup H, with 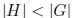. The first case having been
dealt with, we turn to the second. The subgroup H is also a solvable group. Since the groups of
order 2 and 3 are cyclic, what has already been shown applies to them. By induction on 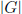, we
can represent all the elements of H as products of subsequences of a sequence of at most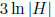
elements. The same is true of the quotient group 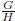, which also has fewer elements than G and is
solvable. Choosing one representative from the right coset of each element in a suitable sequence
of at most 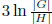elements of the quotient group, and adjoining these to the previous sequence,
we can then represent all the elements in the group as products of subsequences of a sequence of
at most

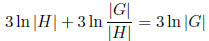
elements.
This stronger result holds in particular for all groups of odd order and all commutative groups.

Problem B1

What is the maximum number of rational points that can lie on a circle in R² whose center is not
a rational point? (A rational point is a point both of whose coordinates are rational numbers.)

Solution: The maximum number is 2. If 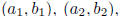and 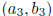are any three points on a
circle, the coordinates of the center of that circle are rational functions of the six coordinates of
these three points. Hence if there are three rational points on a circle, its center is also a rational
point.

There can be two rational points on a circle whose center is not a rational point. For example,
the circle about 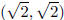of radius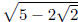, whose equation is

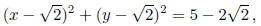
passes through (1, 0) and (0, 1).

Problem B2

Let F₀(x) = ln x. For n ≥ 0 and x > 0, let 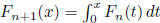. Evaluate .

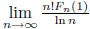Solution: The limit is -1. It is easy to prove by induction that

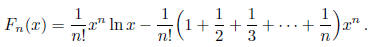
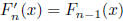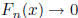(For , and as x 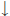0.) Hence,

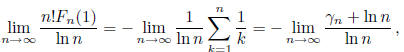
where 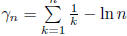tends to the finite limit 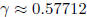, Euler's constant.

Problem B3

What is the largest possible radius of a circle contained in a 4-dimensional hypercube of side length
1?
Solution: The maximum radius is .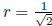

Let 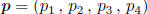and 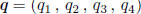be any two points lying on a given circle of
radius r contained in a hypercube of side 1 with a 90° arc between them. Let
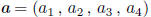
be the center of the circle.

Then the circle can be represented parametrically as

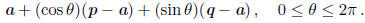
The projection of this circle on the jth axis is parameterized as the locus of all points

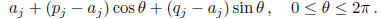
This locus is the interval 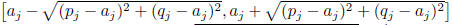. Since the
length of this interval is at most 1, we must have 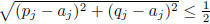, that is

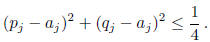
But the radius r is given by

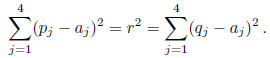
It follows that 2r² ≤ 1, or .
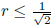To see that this bound can be attained, let us take the hypercube to be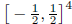. The circle
of radius 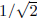with center at (0, 0, 0, 0) in the hyperplane spanned by the mutually perpendicular
unit vectors 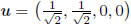and 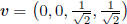(which are not themselves contained in the
hypercube) is given by the parametric mapping

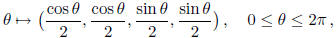
and is obviously contained in the hypercube.

Problem B4

Let p be a prime number. Let h(x) be a polynomial with integer coefficients such that h(0), h(1),... ,
h(p² - 1) are distinct modulo p². Show that h(0), h(1),... , h(p³ - 1) are distinct modulo p³.

Solution: Let 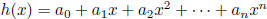, where 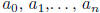are integers.
Let r be any nonzero integer. We observe that r divides h(k + r) - h(k), since it divides
(k + r)^t - k^t for all nonnegative integers t.

Suppose k and l are integers 0 ≤ k ≤ l < p³ such that p³ divides h(k)-h(l). Write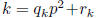
and 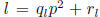, where 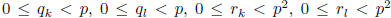. Since p² divides
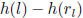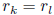h(k) - h(r_k) and , it follows that p² divides . But this means , and
so, sinc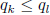e , we must have l = k + mp², where 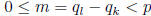. We wish to show m = 0,
which is equivalent to showing that p divides m.

Now p³ divides h(k + mp²) - h(k). Observe that for some integer N we have

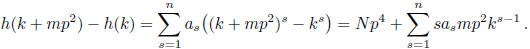
It follows that p divides

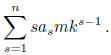
In the latter case, we find that for some integer M,

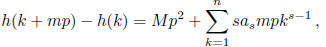
and so p² divides h(k +mp)-h(k). Now choose u and v such that 0 ≤ u < p², 0 ≤ v < p², and p²
divides both k + mp - u and k - v. It then follows that p² divides h(u) - h(v), so that u = v. But
then p² divides k + mp - u - (k - v) = mp. That is, p divides m, as we wished to show.