Sample Exam 3 problems solved

The following problems should be studied to prepare for the third exam.
Do learn the meaning of what is being calculated, rather than just the formal
wording of the question.

Be sure to memorize all the 11 formulas in the trigonometry section of
your formula pages. You should be prepared to know these formulas by name
and reproduce them for credit, as shown in the solutions below.

Curve Fitting.
(a) Points A(1, 16),B(2, 13),C(-2, 1) are on the graph of the quadratic
function f(x) = ax^2 + bx + c. Find a, b, c.

Answer:
Substitute the given points in the equation y = f(x) to get three
equations.

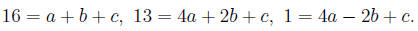
Now solve these to find (a, b, c). Write down the resulting f(x).
Simply subtracting the first from the rest, you get:

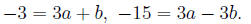
It is easy to solve these two to get a = -2, b = 3. Plugging back
into the first equation, you get c = 15.

Report:a = -2, b = 3, c = 15. Thus f(x) = -2x^2 + 3x + 15.

(b) The function f(x) = ax^2 + bx + c has roots 3, 4 and its graph
passes through (5, 6). Find a, b, c. Decide if the graph of y = f(x)
opens up or down. Find its vertex.

Answer: From the given roots, using the "Remainder Theorem"
(page 68), we deduce that f(x) must have factors (x - 3) and
(x - 4). Thus, f(x) = a(x - 3)(x - 4).

Then the given point (5, 6) gives 6 = a(5 - 3)(5 - 4), so a = 3.
Thus we have f(x) = 3(x - 3)(x - 4) = 3(x^2 - 7x + 12) = 3x^2 -
21x + 36.

Because the leading coefficient 3 is positive, the graph of y = f(x)
opens up.

The vertex of the parabola y = f(x) can be now found to have x-coordinate

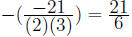
This can also be done from the known theory that it is the average
of the two x-intercepts 3, 4 and thus is

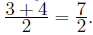
the y-coordinate of the vertex (also the absolute minimum value
of f(x)) is then

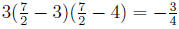
(c) The equation of the circle passing through points A(3, 0),B(0, 3),C(-1, 2) is:

Answer:
Assume that the equation is in a standard form x^2+y^2+ux+vy =
w. Substitute the three points to get three equations:

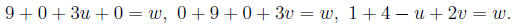
Solve as before to get u = -2, v = -2,w = 3. Thus the equation
is: x^2 + y^2 - 2x - 2y = 3.

Inverse function.
If f(x) = 5 - 7x then the inverse function f^-1(x) is:

Answer: Recall:
Set y = f(x) and solve the equation for x. If you get an unambiguous
solution then the inverse exists.

Thus, solve y = 5 - 7x. Thus 7x = 5 - y or x =

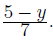
Since this is unambiguous, we have the inverse funciton which satisfies

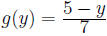
Then by a simple substitution,

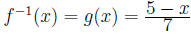
Circle Problems.
(a) The center and the radius of the circle x^2 +y^2 +4x-7y = 30 are:

Answer: If the circle is x^2 + y^2 + ux + vy = w then the center is

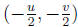The radius is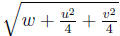Formula: Geometry(17)
Thus:

Center is:

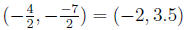
Radius is:

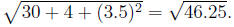
(b) If A(5, 11),B(4,-7) are given, what is the equation of a circle
with diameter AB?

Answer:
Use the formula Geometry(19): (x-5)(x-4)+(y-11)(y+7) = 0:
If needed, you can simplify this and find the center and radius
using Geometry(17).

(c) Find the two points where the line 2x - 3y = 5 meets the circle
x^2 + y^2 - 4x + 2y = 15.

Answer: Solve the line equation for y, then plug into the circle
equation to get the x-coordinates. Use them and the line equation
to find the y-coordinates.

Thus, we get 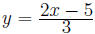Substituting in the circle equation, we get:

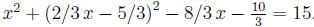
Simplify after moving 15 to the left:

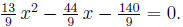
Solve! Use quadratic formula or factoring to get x = -2, 70/13 .If
you are given the easy root, then the factorization is easy, since
you know that (x + 2) is a factor by the Remainder Theorem.
Thus, the two points of intersection are: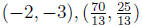

(d) Find the points of intersection of the circles x^2 +y^2 -2x-y = 20
and x^2 + y^2 - 4x + 2y = 15.

Answer: Subtract one circle equation from the other, so that we
get a line and a circle to intersect. Here, if we subtract the second
from the first, we get 2x - 3y = 5.

Thus, the problem is the same as the above problem and has the
same solution.

(e) The equation of the line through the points of intersection of circles

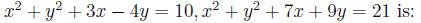
Answer:

Just subtract first equation from the second to get: 4x+13y = 11.
This is a line and passes through the common points (if any!)
No need to find the points of intersection! They are a mess here!

(f) What is the distance of a point A(4, 3) from the line L : 3x-4y = 11?

Is the point B(6, 1) on the same side of L as A or the opposite
side?

Which of A,B is closer to the line?

Answer:
We use the formula Geometry(20).
Be sure to rewrite the equation in a matching form as 3x-4y-11 = 0.
Thus, a=3,b=-4,c=-11.

Thus w = (3)(4)-(4)(3)-11 = -11. The distance is

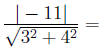
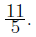
For the final part, calculate the value of w using the point B:
(3)(6) - (4)(1) - 11 = 3. Since 3 and -11 have different signs,
these are on different sides of the line.
The distance of B is 3/5 and hence it is closer to the line than A.

(g) The circle with center at (6, 1) and tangent to the line L : 3x-4y = 11 is:

Answer: Find the distance from the point to the line as before
and set it equal to the radius of the circle.
From above, we know the distance to be 3/5 . So, the circle is:

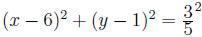
Trig basics
 (a) Given angle t = 773° determine the locator point P(t) and thus
find cos(t), sin(t). Also give s degrees such that s ∈ [0, 360) and
P(s) = P(t).

Answer similar questions using t = -447°.

Answer:
We can subtract 360 twice from 773 to get s = 773 - 720 = 53.
Thus s = 53°.

Thus cos(t), sin(t) are the same as cos(53°), sin(53°). These can
be evaluated by the calculator to be 0.60182, 0.79864.
For t = -447 we add 360 twice to get s = 720-447 = 273. Its trig
functions are: cos(273°), sin(273°) = (0.052372,-0.99863), using
a calculator.

(b) In a circle of radius 20, the arclength from point A to B is 25.
What is the angle subtended by AB at the center of the circle?
Give the angle in radians as well as dgrees.
The angle is also described as the angle between the two radii at
A,B respectively.

Answer,
In radians, the answer is obtained by dividing the arclength by
the radius, so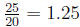

The degree measure is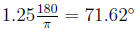

(c) If the radius of a circle is 20 and angle between two radii is 50°,
then calculate the length of the chord between them and also the
area of the resulting triangle.

Answer: By dropping a perpendicular from the center of the
circle to the chord, it is easy to deduce that the chord length is
2r sin( t/2 ), when t is the angle between the radii and r is the radius.
Thus, the chord length is 2(20) sin(25°) = 16.905

This is the base of the resulting triangle and its height is seen to
be given by the formula r cos( t/2 ).
Thus, the formula for the area is:

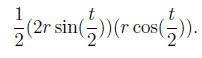
A simple manipulation and use of the formula Trigonometry(8) gives:

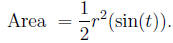
In our case, this gives 153.21.

(d) You are given the locator points for some angles below. Using
them along with appropriate trigonometric formulas, determine
the other locators points as asked. It is necessary to state the
appropriate formula and evaluate the resulting expression.
A direct calculator evaluation will earn negative points!
Given:

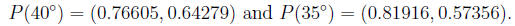
i. Find P(75°).

Answer: Since 75 = 40 + 35, we use the addition formulas
Trigonometry(3,4).

Thus cos(x + y) = cos(x) cos(y) - sin(x) sin(y) and hence
cos(75) = cos(40) cos(35) - sin(40) sin(35)

So
cos(75) = (0.76605)(0.81916)-(0.64279)(0.57356) = 0.25884.
Similarly, sin(x+y) = sin(x)cos(y)+cos(x)sin(y) and hence
sin(75) = sin(40) cos(35) + cos(40) sin(35)

So
sin(75) = (0.64279)(0.81916)+(0.76605)(0.57356) = 0.25884.

Thus P(75°) = (0.25884, 0.25884). Note that a bit of accuracy
can be lost due to calculation steps and hence it is sometimes
desirable to make the original values more precise!

ii. Find P(5°).
Answer: Since 5 = 40 - 35, we use the addition formulas
Trigonometry(3,4), but with a -y in place of y.
Using formula Trigonometry(6) we get subtraction formulas:

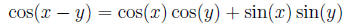
and

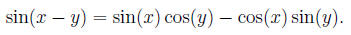
Thus

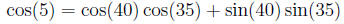
So

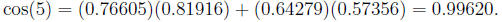
Similarly

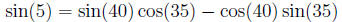
So

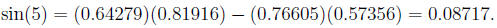
Thus, P(5°) = (0.99620, 0.08717).

iii. Find P(70°).

Answer:
We note that 70 = (2)(35). So, the double angle formulas
Trigonometry(7,8) come in handy.
We have

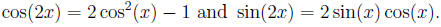
using these, we get:

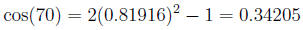
and

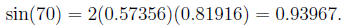
Thus, P(70) = (0.34205, 0.93967).

iv. Find P(20°).
Answer:
We note that 20 = 1/2(40). So, we use the half angle formulas
Trigonometry(9).
Thus

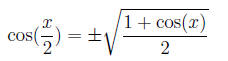
and

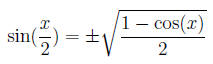
where the signs are to be determined by the quadrant where
the angle lives.
Note that 20° is in the first quadrant since it is a number in
the interval (0, 90). Thus we have plus signs in both formulas.
Thus

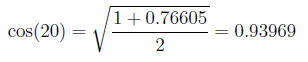
and

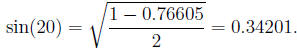
(e) Write the complex number 4 - 5i as re^it.
Answer similar question for -4 + 5i.

Answer:

Note that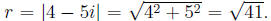It is not necessary to
simplify further to the decimal 6.40312.

The angle t is found from t = arctan(-5/4 ) = -0.89606.

This calculation works when the real part (4 in this case) is positive.

The second number -4+5i is best handled by noting the e^iπ = -1,
so that

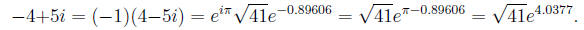
(f) Be sure to memorize the 10 Trigonometry formulas, by name if
appropriate so you can use them as needed.

Trig uses (a) The top of a building is sighted at an elevation of 17.354° at a
certain distance from the building and the elevation angle goes down
to 16.389 if the observer walks 100 ft. away from the building.
What is the height of the building?

Answer:

The problem is very similar to the sample on page 176, although
it is slightly different in the wording.
We let h be the unknown height of the building and let d be the
original distance from the building.

Then we see two equations:

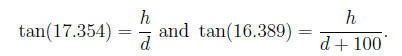
Rearranging the equations, we get:

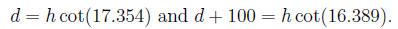
Subtracting the first from the second, we eliminate d to get: 100 =
h(cot(16.389) - cot(17.354)).
This gives the answer:

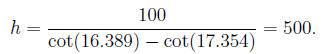
(b) Find the angle between the hour and the minute hand of an analog
twelve hour clock when the time is 25 minutes past 9.

Answer:

Note that the angle between two successive hour markers is 30
degrees. Thus, the hour hand must be (30)*( 25/60 ) degrees past
the 9-th hour marker. The minute hand must be pointing to the
5-th hour marker. The angle between the 5-th and the 9-th hour
marker is clearly (30)*(9-5) = 120 degrees. Thus the total angle is

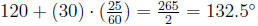
Note that the angle can be measured clockwise or counter clock-
wise. The general convention is to use the one which is smaller
than 180° .

(c) A triangle ABC has side AB equal to 10 units. If the adjacent
angles A,B are respectively 30 and 40 degrees, what are the other
two sides and the remaining angle.

Answer:

First, we know that the remaining angle is 180 - 30 - 40 = 110 degrees.
the Sine Law Trigonometry(10) says:

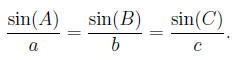
We are given A,B, c and have deduced C. Thus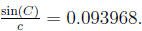

Then we get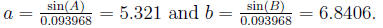

(d) A triangle ABC has side AB equal to 10 units and side AC equal
15 units. If the angle A between them is 40 degrees, then find the
third side BC (or a in the usual notation).
Use it to determine the other two angles B,C.

Answer: We use the Cosine Law Trigonometry(11).
Thus:

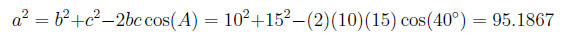
and hence

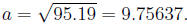
To find the other angles, we may try to use the Sine Law, but
there is a potential problem. If we know the sine of an angle we
have two possible angles between 0 and 180 degrees which give
the same sine. We have to look carefully to decide the quadrant.
It is safer to use the Cosine Law again.

Thus we have:

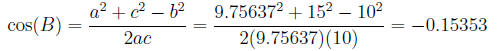
and using arccos this gives B = 98.8313° .

Indeed, this minus sign indicates that the angle is in the second
quadrant and if we were to look at the sine of the angle it would be
positive and we would get the wrong angle (in the first quadrant).
Similarly, we have:

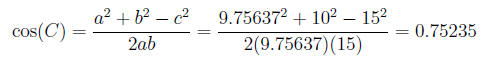
and using arccos this gives C = 41.2056° .