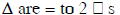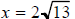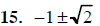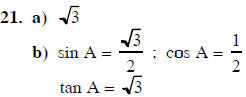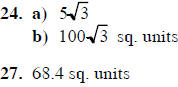MATH 1175 COURSE REVIEW #1
1. Simplify: 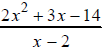
2. Solve for x: 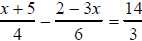
3. Solve for x: 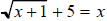
4. Combine in each example below:

5. Rationalize the denominators in each example below:

6. Solve graphically:
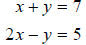
7. Solve using the quadratic formula: 2x2−2x−1=0
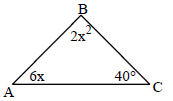
8. Find x, ∠A, and ∠B
|
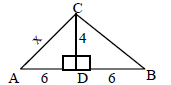
9. a) Why are ΔACD and ΔBCD congruent? b) Find x c) Find the area of ΔABC |
 |
10. Simplify:
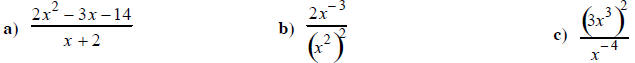
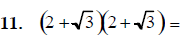
12. Solve for x: 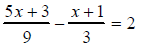
13. Simplify: 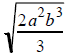
14.
a) Divide by long division:
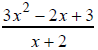
b) Combine: 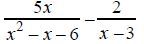
15. Solve using the quadratic formula: x2+2x−1=0
| 16. Find x, AB, BC, and AC |
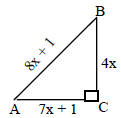 |
|
17. a) State the relationship of ΔABC to ΔADE b) Find x, AB, AD, BC, and DE |
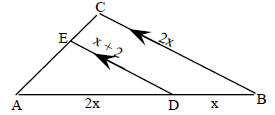 |
|
18. Find x, y and the area of the rectangle. Leave answers to the nearest tenth. sin 53° = .7986 cos 53° = .6018 tan 53° = 1.3270 |
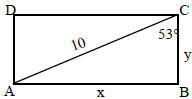 |
|
19. a) Find the area of the square ABCD. b) Find the area and the circumference of the circle. c) Find the area of the shaded part. |
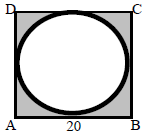 |
|
20. a) Why are ΔABD and ΔCDB congruent? b) Which sides of the congruent triangles are equal? c) Find x and y. |
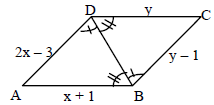 |
|
21. a) Find x b) Find sin A, cos A, and tan A. |
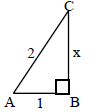 |
|
22. a) Find x and y (to the nearest tenth) b) Find the area of ΔABC sin 50° = .7660 cos 50° = .6428 tan 50° = 1.1918 |
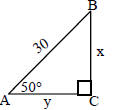 |
|
23. a) What is the relationship which exists between Δ ABC and Δ EFG? b) Find x. |
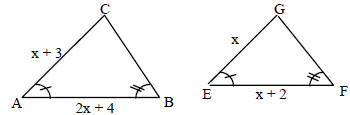 |
|
24. a) Find x (leave the answer in radical form) b) Find the area of the parallelogram ABCD. (Leave the answer in radical form) |
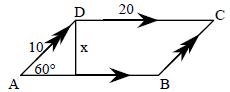 |
|
25. a) Find x and y b) Find AB and BC |
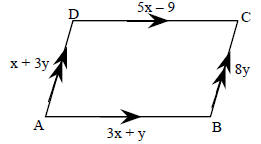 |
|
26. a) Explain why ΔDEC is similar to ΔABC. b) Find x |
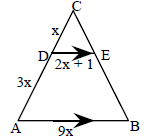 |
|
27. Find the area of the parallelogram ABCD to the nearest tenth, if BE ⊥ AD, ED = 8, BC = 12, ∠A = 55° sin 55° = .8192 cos 55° = .5735 tan 55° = 1.4281 |
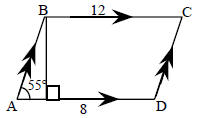 |
ANSWERS:
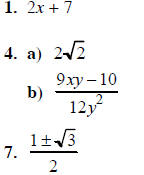
16. x = 2; AB = 17; BC = 8; 19. 22. 25.
|
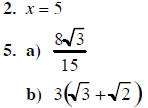 8. x =
7; x = – 10 (reject)
17. 20. 23. 26. |
3. x = 8; x= 3 (reject) 6. (4, 3) 9. 12. x = 9
18. x = 8; y = 6; Area = 48 sq.
|


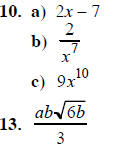
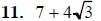
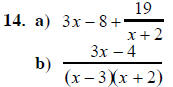
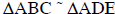 (triangles
(triangles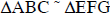 (similar)
(similar)