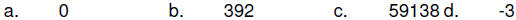Sidebar Menu
Topics in Computer Mathematics - Number Systems
BCD numbers.
In some applications, such as in the financial industry, the errors that can
creep in due to
converting numbers back and forth between decimal and binary is unacceptable.
For
these applications it is common to represent decimal numbers in format called
‘Binary
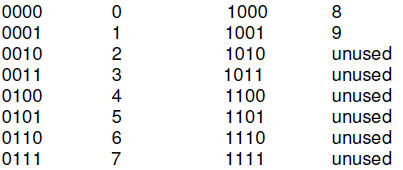
Coded Decimal’, or BCD. In this format, each decimal digit is converted to its
binary
equivalent. Thus, each decimal digit uses 4 bits, and only the binary values
0000 thru
1001 are used, as in the following table.
Since each decimal digit uses 4-bits, a byte can only hold
two digits. A 5 digit decimal
number uses 2 ½ bytes. It is common to allocate space for an odd number of
digits; this
leaves ½ of a byte left over for the sign so that BCD numbers often are
expressed in
sign & magnitude format. (It is also possible to use 10's complement or 9's
complement
formats.)
Examples:
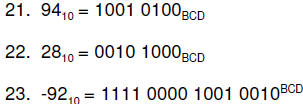
The above examples are more properly called Packed BCD
numbers because two digits
are ‘packed’ into a single byte. This format is usually used for storing BCD
numbers, but
for actually performing arithmetic an unpacked BCD format is generally used.
This
format devotes an entire byte to each decimal digit, with the high order four
bits equal to
0's, except for the first byte, which might indicate the sign of the number in
sign &
magnitude notation
Examples:
| Practice Problems - BCD format 1. Express the following Decimal numbers in packed BCD format:
2. Express the following Decimal numbers in unpacked BCD format:
3. What decimal number, if any, is represented by
each of the following packed
4. What is the maximum unsigned decimal number
which can be represented in |
Floating point numbers
Floating point numbers are used wherever very large or very small numbers need
to be
manipulated, such as in cosmological physics, or quantum physics, or other
scientific
disciplines. This notation is also called scientific notation, or engineering
notation.
In general usage, a floating point number is represented by a fraction
multiplied by the
base raised to a power. For instance, given the fixed point number
3456.231,
this could be represented in scientific (floating point) notation as
It could also have been represented by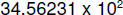 
or
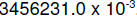It is
conventional, however, to ‘normalize’ a number so that there is just one
non-zero digit to
the left of the decimal point. Hence, [N12] is the ‘correct’ form of this
number. Note that
both the number itself as well as the exponent may be negative. E.g.
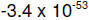
Nomenclature: The normalized digits are referred to as the ‘mantissa’ (I
have taken
some liberties here, as usually the mantissa only refers to the digits to the
right of the
decimal point). The exponent is called the ‘exponent’.
The advantage of this representation is the range of numbers that can be
represented.
Remember that an n-digit decimal integer is restricted to the range 0 through
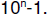(e.g.
a 3 digit number goes from 0 through 999). If the n digits are all fractional
digits, the
numbers representable are 0 through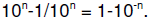 
(Note
that only numbers with n
significant digits can be represented, so the entire continuum of fractions in
this range
can not be represented. A three digit fraction can represent .000 through .999,
but not,
say, .9985). In floating point notation, in addition to the number of
significant digits of
the mantissa, the decimal point can be placed anywhere in the allowable range of
the
exponent.
In a computer system, the exponent as well as the mantissa is held in a storage
location
or register with limited extent. Let’s assume that (still considering decimal
numbers) the
mantissa is given by 4 digits and the exponent is given 2 digits. Then the
numbers that
can be represented in this format (ignoring the signs for the time being are)
0.000 through 9.999 for the mantissa, and
00 through 99 for the exponent.
The smallest number (ignoring signs) is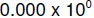 
and
the largest is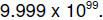 
If we
sketch out the numbers on the real line, we see that there are gaps where
nonrepresentable
numbers exist. For instance, none of the numbers between
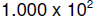
and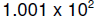 
can be represented. Even more interesting
is the fact that none of the
numbers immediately following 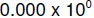(zero) are
representable, such as 0.0001, so
the first gap is right at the origin of the real line. For each exponent, the
gaps are
uniformly spaced and of uniform size, but as the exponents increase the gaps get
bigger
. In general, every individual number is separated by from every other one by a
gap.
Additionally, every exponent range is separated from each other by a gap. As
numbers
move farther from zero, these gaps get larger.
Example: consider
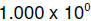and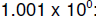 
they
differ by .001. But
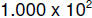and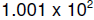 
differ by .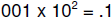
We should expect something like this since it should be obvious that in a finite
number
of bits only a finite number of numbers can be represented, despite the fact
that in any
range of real numbers there are an infinite number of them.
We will now discuss the actual representation of floating point numbers in a
computer
system - binary floating point numbers and how they are stored in hardware
registers.
Consider the number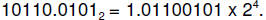 
To implement this in
computer
hardware we need to specify the following:
a. The number of bits allocated to the mantissa
b. The number of bits allocated to the exponent
c. How the sign of the number will be represented
d. How the sign of the exponent will be represented.
In general, all of this information is kept in a single
register, divided up into sections,
called fields:
| Sign | Exponent | Mantissa |
The sign shown is a single bit and refers to the
sign of the entire number (or,
equivalently, of the mantissa.)
The exponent is in biased notation. The reason for this is as follows:
consider two
decimal floating point numbers which you wish to add together, say
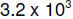and
4.0 x
105. Before they can be added, they must be made to have the same exponent.
(i.e.
we need to align the decimal points). We usually choose the number with the
smaller
exponent and increase it to match the other exponent, moving the decimal point
to the
left a corresponding number of positions. (Moving the decimal point left is
accomplished
in practice by shifting the fraction to the right; in this process some digits
are lost as they
are shifted off the right end of the register - the least significant ones.)
Therefore, we
need to easily be able to increase one or the other of the exponents by a
(usually) small
amount, regardless of whether it is positive or negative, and even if the sign
changes
during the process, as it might. See Table TN3 to see that, of the different
number
representations, only the biased form provides this capability.
The mantissa, or fraction, is the normalized form of the given digits, or as
many of them
as will fit in the allocated space. Remember that a
normalized number, in our
discussion, has a single non-zero digit to the left of the binary point. Since
there is only
one possible non-zero value, one, some savings are realized by not bothering to
actually
waste a bit on that digit - it is always assumed, or implied, that a 1 precedes
the rest of
the fraction. This allows an extra bit of significance to be maintained in the
mantissa
field of the register.
A typical floating point number in this format would look like this:
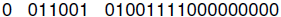(or 329E00 in hexadecimal notation)
where the sign is +, the exponent is 011001 (we haven’t specified the bias) and
the
mantissa is 1.01001111000000000 (note that we have added the implied one to the
left
of the binary point.) Notice that this format does not allow you to represent a
value of
zero! If we are given
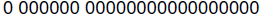
we should interpret this as an exponent of 000000 but a mantissa of
1.00000000000000000. It is usual, however, to treat zero as a special case: When
all
the bits in the representation are 0's, as in this last example, then the number
is
assumed to be zero and no implied 1 is included when interpreting the number.