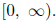Sidebar Menu
Combinations of Functions
1 Combinations of Functions, §1.5
Sums, Differences, Products, and Quotients of Functions: Let f and g
be two functions
with overlapping domains. Then, for all x common to both domains, the sum,
difference,
product, and quotient of f and g are defined as follows.
Sum: The domain is the intersection of the domains f and g.
(f + g) (x) = f (x) + g (x)
Difference: The domain is the intersection of the domains f and g.
(f − g) (x) = f (x) − g (x)
Product: The domain is the intersection of the domains f and g.
(f · g) (x) = f (x) · g (x)
Quotient: The domain is the intersection of the domains f and g, but
we must exclude the x’s
in g’s domain where g (x) = 0.
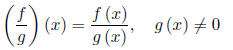
1.1 Examples
1. Given f (x) = 2x − 3 and g (x) = 3x2 + 2x − 5, find each of the following.
(a) The domain of f (x).
(b) The domain of g (x).
(c) f (x) + g (x) and its domain.
(d) f (x) − g (x) and its domain.
(e) f (x) · g (x) and its domain.
(f) f (x) /g (x) and its domain.
2. Given
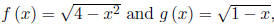find each of the following.
(a) The domain of f (x).
(b) The domain of g (x).
(c) f (x) + g (x) and its domain.
(d) f (x) − g (x) and its domain.
(e) f (x) · g (x) and its domain.
(f) f (x) /g (x) and its domain.
2 Composition of Functions, §1.5
The Composition: of the function f with the function g is
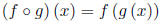
The domain of
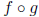is the set of all x in the domain of g such that g (x), i.e. the range of g, is
in the domain of f,
2.1 Examples
1. Given
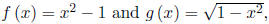find each of the following.
(a) The domain of f (x).
(b) The domain of g (x).
(c) The range of f (x).
(d) The range of g (x).
(e)
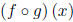and its domain.
(f)
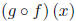and its domain.
2. Given
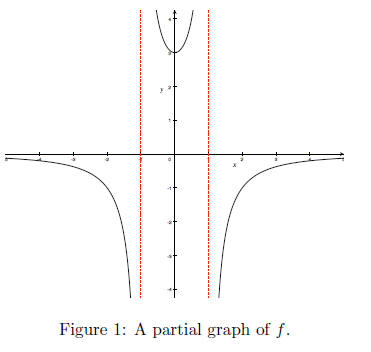
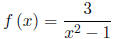and g (x) = x + 1, find each of the following. A graph of f is given
(following page) to help determine f’s range.
(a) The domain of f (x).
(b) The domain of g (x).
(c) The range of f (x).
(d) The range of g (x).
(e)
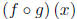and its domain.
(f)
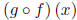and its domain.
3 Inverse Functions, §1.6
Definition: A function f is called one-to-one if it never takes on the same value twice; that is
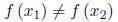
whenever
.
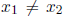We can often visually verified that a function is one-to-one by using the
horizontal line test, which states, “A function is one-to-one if an only if no
horizontal line
intersects its graph more than once. For example, the following function is not
one-to-one.
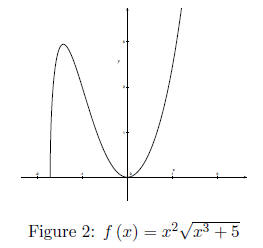
However, this function is one-to-one.
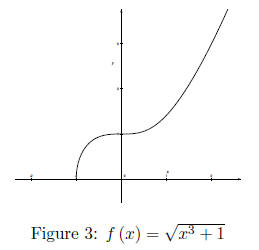
Some however may be mislead by the horizontal line test, because it is hard
to detect from
the visual alone that
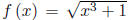is one-to-one. It should be clear though that f (x) =
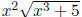is not one-to-one from the graph alone. To show that
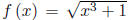is one-to-one
we proceed as follows. Since for all
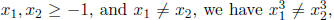which further
implies that
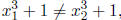and finally that
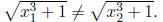
Definition: Let f be a one-to-one function with domain A and range B.
Then its inverse
function f−1 has a domain B and range A and is defined by
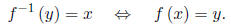
To find the inverse of a one-to-one function, follow these steps.
1. In the equation for f (x), replace f (x) by y.
2. Interchange the roles of x and y, and solve for y.
3. Replace y by f−1 (x) in the new equation.
4. Although not necessary, you may want to verify that
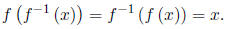
Let’s start with a simple example. Given a one-to-one
function, f (x) = 2x−1, find its domain,
range, and inverse.
Work:
First off we know f is one-to-one with domain x ∈R and range f (x) ∈R, so its
inverse, denoted
f-1 (x), has a domain x ∈R and range f-1 (x) ∈R. Using simple algebra (method
above) to
find f-1 (x).
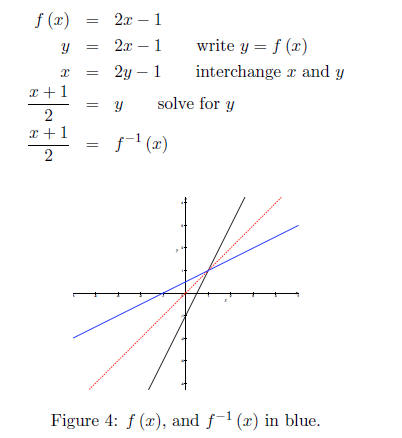
You should observe the symmetry along the line y = x.
Here’s a more difficult example, however it is still
algebraically manageable. Using f (x) =
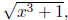let’s find its inverse. First off we know f
is one-to-one with domain x≥−1 and range
f (x)≥0, so its inverse, denoted f-1 (x), has a domain x≥0 and range f-1 (x)≥
−1. Using
simple algebra to find f-1 (x).
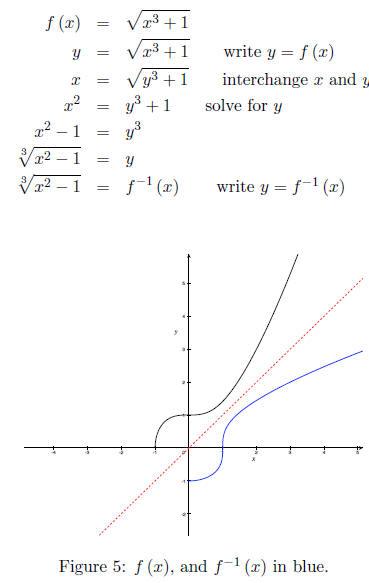
You should observe the symmetry along the line y = x.
An even more difficult example, given,
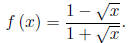
find f-1 and its domain and range. A graph is provided as a visual aid.
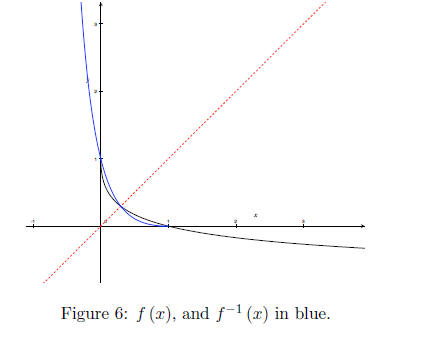
Work:
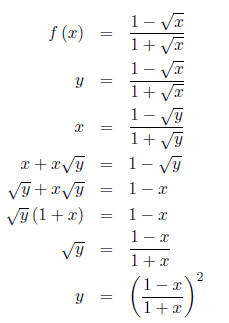
We finally have,
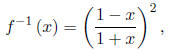
and its domain is (−1 1] and its range is
