Finite Mathematics for the Life and Social Science

Read all of the following information before starting the exam.

You have 2.5 hours to complete this exam. Please read all instructions carefully, and check your
answers. Show all work neatly and in order, and clearly indicate your final answers. Answers
must be justified whenever possible in order to earn full credit. Unless otherwise specified,
no credit will be given for unsupported answers, even if your final answer is correct.
Points will be deducted for incoherent, incorrect, and/or irrelevant statements.

Calculators are permitted, however, you will still need to show your work in any problem involving
systems of linear equations, matrix multiplication, or matrix inverses. There is an attached
page of . A copy of Table 1 from the textbook will also be provided. There are no other
aids allowed.

This test has 10 numbered pages with 9 questions totalling 150 points. Before you hand in your
exam, make sure you have all of the pages.

Do not detach this page from the exam booklet

Least Squares Line
The least squares line Y = mx+b that gives the best t to the data points (x₁, y₁), (x₂, y₂), … , (x_n, y_n)
has slope m and y-intercept b that satisfy the equations

Coefficient of Correlation

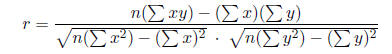
Bayes' Theorem

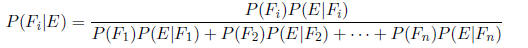
Standard Deviation
The standard deviation of the n numbers x₁, x₂, x₃, … , x_n, with mean 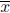, is

Mean and Standard Deviation for Binomial Distribution
For the binomial distribution, the mean and standard deviation are given by

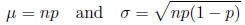
where n is the number of trials and p is the probability of success on a single trial.

Absorbing Markov Chains
If the transition matrix for an absorbing Markov chain is

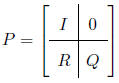
then the associated fundamental matrix is

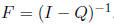
1. (10 points) Spencer wants to make money by selling test preparation guides for Math 105.
He estimates it will require $50 to write the guide, and each guide will cost $2 to print.

(a) What is the cost function for Spencer's venture?

 

(b) If Spencer sells guides for $3 each, how many must he sell to break even?

 

2. (10 points) Suppose that, for two events E and F, we have P(E) = 0.4 and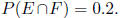
(a) Find a value for P(F) so that E and F will be independent events.

 

(b) Using your answer to (a), determine

 

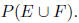
3. (12 points) Suppose Melanie has forty tacos, and that she selects one of these tacos at
random. Let J be the event that the taco has peppers, and let G be the event that the
taco has green onions. Suppose further that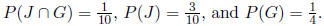

(a) How many of the forty tacos have neither peppers nor green onions?

 

(b) Suppose the one taco Melanie chooses has green onions on it. What is the probability that
it does not have 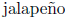peppers?

 

4. (16 points) Use the row echelon or Gauss-Jordan method to solve the equations:

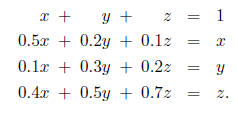
5. (18 points) The Cornell University Dairy Bar Medical Center did a study of hereditary
patterns in ice cream preference. They asked generations of families their favorite flavor of
ice cream. They found that if someone preferred strawberry ice cream, their children had a
probability of 0.5 of preferring strawberry ice cream, a probability of 0.1 of preferring chocolate
ice cream, and a probability of 0.4 of preferring vanilla ice cream. If someone preferred chocolate
ice cream, their children had a probability of 0.2 of preferring strawberry, a probablility of 0.3 of
preferring chocolate, and a probability of 0.5 of preferring vanilla. If someone preferred vanilla,
their children had a probability of 0.1 of preferring strawberry, a probability of 0.2 of preferring
chocolate, and a probability of 0.7 of preferring vanilla.

(a) Write the transition matrix P for the above Markov chain. Is this a regular Markov chain?

 

(b) Find the equillibrium vector, and clearly show why it is the equillibrium vector. (Hint:
use problem 4.)

 

(c) If Jay prefers chocolate ice cream, what is the probability that his grandchild will prefer
vanilla ice cream?

 

6. (20 points)

(a) Find the inverse of

 

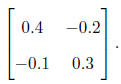
6(b) Consider a Markov chain which has four states called A, B, C, and D. Let its transition
matrix P be given below. (Let the states A, B, C, and D correspond to the 1st, 2nd, 3rd,
and 4th rows and columns, respectively.)

If the Markov chain starts in state C, what is the probability that it will eventually end
up in state A?

 

7. (20 points) In the movie Casablanca, Rick complains because Ilsa, an ex-girlfriend of his,
comes to the bar he owns. \Of all the gin joints in all the towns in all the world, she walks into
mine," he says. In an overly simplified (and incorrect!) model, suppose that the world has only
200 towns, each with 10 gin joints.

(a) What is the probability that Ilsa walks into Rick's bar? (Assume that her choice of both
town and gin joint is random, and that each choice is equally likely.)

 

(b) Suppose six of Rick's ex-girlfriends are (independently) hanging out in the same town
as Rick's bar, and each decides to pick a gin joint in that town to visit. What is the
probability that fewer than three of them come into Rick's bar?

 

(c) Suppose 100 of Rick's ex-girlfriends are hanging out in the same town as Rick's gin joint.
If each one independently picks a gin joint from the ten available, use the normal approximation
to estimate the probability that more than eleven of his ex-girlfriends choose Rick's
bar?

 

8. (20 points) The Egalitarian Theater Company (ETC) chooses actors randomly without
regard to race, gender, age, or acting ability.

(a) If 20 people audition for 12 Angry Men, how many ways can the ETC cast the 12 different
characters?

 

(b) The remaining 8 people will be on the lighting crew, sound crew, and props crew. If two
are chosen for lighting, two for sound, and the remaining four for props, how many ways
can the ETC assign these eight people?

 

(c) If Mike is one of the 20 people auditioning, what is the probability that he is cast as an
Angry Man?

 

(d) If 17 of the 20 people auditioning are women, what is the probability that all of the Angry
Men are women?

 

9. (24 points) Four nickels and six dimes are tossed. Let X be the total number of heads
observed, and let Y be the total worth (in cents) of all the coins which show heads. (Note that
the possible values of X are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 and that the possible values of Y are
0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80.)

(a) Compute E(X), the expected value of X.

 

(b) Compute P(X = 3).

 

(c) Compute P(Y = 15).

 

(d) Suppose that exactly 3 heads are observed. What is the probability that their values sum
to 15 cents?