Functions and Difference Quotients Review
I. Composition of Functions
II. Difference Quotients
Practice Problems
I. Composition of Functions
HAPPY BIRTHDAY... OK so in all likelihood today isn't your birthday.
Let's assume it is and you've been given a present wrapped in a large box.
You open the box and surprise!!!, inside is another box. Undaunted you
open it and discover yet another box. This may appear to be a lesson in ac-
cepting disappointment. Unbeknownst to you, though, you are experiencing
composite function behavior.
HUH?!?! Let us explain.
The composite function is like having one function
contained inside another.
When you see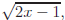 you probably think of it as just
another function,
you probably think of it as just
another function,
but it's something more. It's a composite (one function inside another).
Here's why.
Suppose 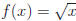 and g(x) =
2x−1 (think of
and g(x) =
2x−1 (think of 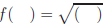 as the larger
as the larger
box). Now place 2x − 1 inside. Mathematically this is written as f(g(x))
and we call it "f composite g". To form a composite, try the following:
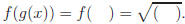
Now ll in the blanks with the g(x) representation and you
get
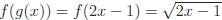
NOTE: just like f(3) means to input 3 into f, f(g(x))
means to input g
into f.
Unlike boxes, any function can be placed inside another.
From above,
g(x) = 2x −1. This really means g( )=2( )− 1. If
![]() . we have
. we have
Alternative notation for composite functions:
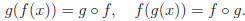
Let's try a different practice drill. Suppose h(x) =
sin(2x). Can you state
functions for f and g so that h = f(g(x))?
Solution: inner function is 2x, which is g,
outer function is sin x = sin( ), which is f.
Check: f(g(x)) = f( )=sin( ).
Now insert 2x and get f(g(x)) = f(2x) = sin2x.
NOTE: This is the most obvious choice for f and g but not
the only
one. Let us try f(x) = sin(x + 1) and g(x) = 2x − 1.
Check: f(g(x)) = f( ) = sin[( ) + 1],
so f(g(x)) = f(2x − 1) = sin[(2x − 1) + 1] = sin 2x.
What's so special about composite functions? One day in
Calc I your
instructor will throw a birthday party for the entire class, and his present
to you will be called the CHAIN RULE.
Exercise: Practice Problem 3.1.
II. Difference Quotients
A. Introduction
In algebra, rate of change is introduced in its most basic
form by finding
the slope of a line using 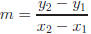 . This "formula"
can also be called
. This "formula"
can also be called
a Difference Quotient. In calculus, rates of change (both average and
instantaneous) are found using function forms of difference quotients.
Let's start with a few examples of the algebra in difference quotients.
Example: Let g(x) = x2 + 1. Evaluate and simplify
the difference
quotient 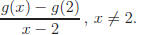
Solution: Using g(x) = x2 + 1 and g(2) = 5,
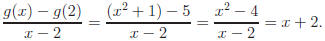
Example: Let 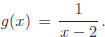 Evaluate
and simplify the difference
Evaluate
and simplify the difference
quotient 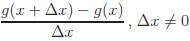 [ Δx represents the "change" in x.]
[ Δx represents the "change" in x.]
Remember: 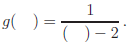

B. Application
How does a difference quotient measure rate of change (or slope)?
Suppose we start with a function f(x) and draw a line (called a secant
line) connecting two of its points.

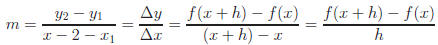
Notice that the slope is represented by a difference
quotient and is
referred to as the average rate of change. Now suppose the distance
between these two points is shortened by decreasing the size of h.

Conclusion: The two points get so close together they
almost con-
cide. The resulting line is now a tangent line whose slope measures the
instantaneous rate of change. You will come to know this slope by the
term "derivative".
PRACTICE PROBLEMS for Topic 3 - Functions and Difference Quotients
3.1 a) Suppose f(x) = x2 − 2x and
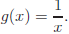 Form the following
Form the following
compositions:
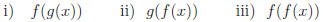
b) Suppose f(x) = sinx and
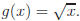 Form the following compositions:
Form the following compositions:

c) Suppose 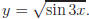 Select
functions for f, g, and h so that
Select
functions for f, g, and h so that
y = f(g(h))(x). Check your results.
Return to Review Topic Answers
3.2 Find the rate of change (slope) of the line containing
the given points.
a) (2,−5) and (4,1)
b) (3,−4) and (3,−1)
c) (x, f(x)) and (x + h, f(x + h))
Answers
3.3 Evaluate and simplify the difference quotient
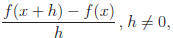 when:
when:
a) f(x) = x2 − 3x,
b) 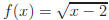 (Rationalize the numerator).
(Rationalize the numerator).
Answers
3.4 Evaluate and simplify the difference quotient
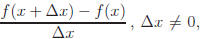
when 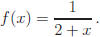
Answers
ANSWERS to PRACTICE PROBLEMS
(Topic 3 - Functions and Difference Quotients)
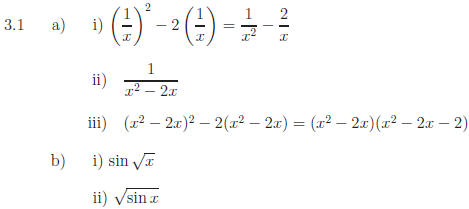
c) inner: h(x) = 3x
middle: g(x) = sinx
outer: 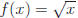
CHECK:
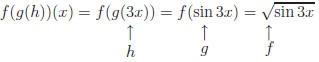
Return to Problem
3.2
a) m = 3
b) m is undefined
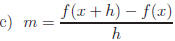
Return to Problem

Return to Problem

Return to Problem
Beginning of Topic
150 Review Topics
Skills Assessment

