Factoring Trinomials of the Form ax^2+bx+c

When trinomials factor, the resulting terms are binomials. Trinomials in the form of ax² + bx + c
where a = 1 will fall into one of three patterns for factoring.

Pattern 1: ax² + bx + c

In this pattern, the coefficient a is positive and both of the operators are addition. This will result
in the product of two monomials, both of which will have operators of addition (+).

ax² + bx + c = (ax + n) (x + m); where n and m are factors of c

Pattern 2: ax² – bx + c

In this pattern, the coefficient a is positive, the operator before b is subtraction (-) and the
operator before c is addition (+). This will result in the product of two monomials, both of which
will have operators of subtraction (-).

ax² – bx + c = (ax – n) (x – m); where n and m are factors of c

Pattern 3: ax² ± bx – c

There are two patterns shown above, either of which will give the same result. The conditions
needed to fit this pattern are that a is positive and that the operator before c is subtraction (-).
The operator before b may be either a subtraction or addition. This will result in the product of
two monomials, one of which will have an operation of addition and one will have an operation
of subtraction.

ax² ± bx – c = (ax + n) (x – m); where n and m are factors of c

Steps in factoring trinomials:

1. Factor out the GCF from the trinomial (if there is one)
2. Determine which pattern applies to the given trinomial
3. Find the factors of the constant term “c” whose sum equals “b”
a. For pattern 1 – both factors need to be positive
b. For pattern 2 – both factors need to be negative
c. For pattern 3 – the factors must be opposite signs
4.Use the factors from step 2 to write the trinomial in factored form
a. If none of the factors work then the trinomial is “prime” and cannot be factored.

Example 1: Factor the trinomial x² + 5x + 6.

Solution:

Step 1: Factor out the GCF from the trinomial (if there is one)

There is no GCF between the three terms of x², 5x, and 6.

Step 2: Determine which pattern applies to the given trinomial.

The operators before the second and third terms are both addition, so this
trinomial fits pattern 1.

ax² + bx + c = (ax + n) (x + m); where n and m are factors of c

Step 3: Find the factors of “c” whose sum equals “b”

Since the factors must be positive the only factors of 6 are 1, 2, 3, and 6.

Factors of 6	Sum of the factors

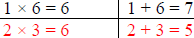The factors of 2 and 3 will give us the coefficient “b” in the trinomial.

Step 4: Use the factors from step 3 to write the trinomial in factored form

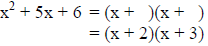
Example 2: Factor the trinomial x² – 7x + 12.

Solution:

Step 1: Factor out the GCF from the trinomial (if there is one)

There is no GCF between the three terms of x², 7x, and 12.

Step 2: Determine which pattern applies to the given trinomial.

The operator before the second term is subtraction and the operator before the
third term is addition, so this trinomial fits pattern 2.

ax² – bx + c = (ax – n) (x – m); where n and m are factors of c

Step 3: Find the factors of “c” whose sum equals “b”

Since the factors must be negative the only factors of 12 are -1, -2, -3, -4, -6, and
-12

Factors of 12	Sum of the factors

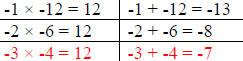The factors of -3 and -4 will give us the coefficient “b” in the trinomial.

Step 4: Use the factors from step 3 to write the trinomial in factored form

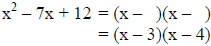
Example 3: Factor the trinomial x² – 10x – 24.

Solution:

Step 1: Factor out the GCF from the trinomial (if there is one)

There is no GCF between the three terms of x², 10x, and 24.

Step 2: Determine which pattern applies to the given trinomial.

The operators before the second and third term are subtraction, so this trinomial
fits pattern 3.

ax² – bx – c = (ax + n) (x – m); where n and m are factors of c

Step 3: Find the factors of “c” whose sum equals “b”

Since the factors must be opposite signs the factors of 24 are ±1, ±2, ±3, ±4, ±6,
±8, ±12, and ±24.

Factors of -24	Sum of the factors

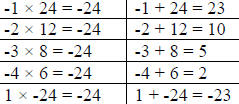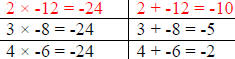The factors of 2 and -12 will give us the coefficient “b” in the trinomial.

Step 4: Use the factors from step 3 to write the trinomial in factored form

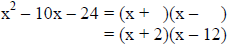
Example 4: Factor the trinomial 2x² – 4x – 6.

Solution:

Step 1: Factor out the GCF from the trinomial (if there is one)

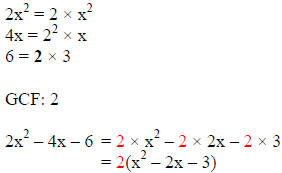
Step 2: Determine which pattern applies to the given trinomial.

Using are remaining trinomial (x² – 2x – 3), the operators before the second and
third term are subtraction, so this trinomial fits pattern 3.

ax² – bx – c = (ax + n) (x – m); where n and m are factors of c

Step 3: Find the factors of “c” whose sum equals “b”

Since the factors must be opposite signs the factors of 3 are ±1 and ±3.

Factors of -3	Sum of the factors

The factors of 1 and -3 will give us the coefficient “b” in the trinomial.

Step 4: Use the factors from step 3 to write the trinomial in factored form

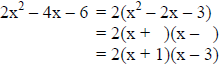
Example 5: Factor the trinomial x² + 8x + 20.

Solution:

Step 1: Factor out the GCF from the trinomial (if there is one)

There is no GCF between the three terms of x², 8x, and 20.

Step 2: Determine which pattern applies to the given trinomial.

The operators before the second and third terms are both addition, so this
trinomial fits pattern 1.

ax² + bx + c = (ax + n) (x + m); where n and m are factors of c

Step 3: Find the factors of “c” whose sum equals “b”

Since the factors must be positive the factors of 20 are 1, 2, 4, 5, 10, and 20.

Factors of 20	Sum of the factors

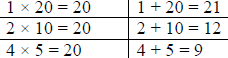None of the factors will give us the coefficient “b” so this trinomial is “prime”
and cannot be factored.

x² + 8x + 20 is prime