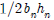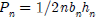Early Greeks & Aristotle
II. The Method of Exhaustion (Eudoxus and Archimedes)
Euclidean Geometry: Two notions of the infinite:
 |
(a) infinite divisibility of line segments (b) infinite extendability of line segments |
| lead to paradoxes of infinitely small and infinitely big |
| BUT: Early Greeks tended to avoid talk of the infinite. In geometry, all objects are really |
 |
finite (like natural numbers: any one is finite; together are all
infinite) |
|
Example: Method of Exhaustion (Eudoxus 408-355 BC) as used by Archimedes to prove area of circle = πr2. |
Let C be a circle with radius r.
For each natural number n, let
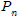 be a regular polygon inscribed in C. be a regular polygon inscribed in C. |
||
|
|
n equal sides and n equal angles |
|
Divide 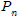 into n
congruent triangles into n
congruent triangles |
|
|
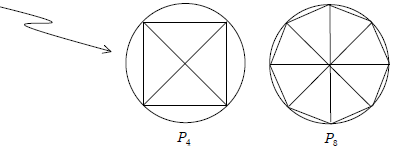
Let
THEN: area of triangle = |
 |
Now visualize C as 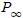 --
a polygon with infinitely many infinitely small sides.
--
a polygon with infinitely many infinitely small sides.
SO: When n = ∞:
 |
The height of each (infinitely thin!) triangle in 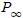 is isidentified with the radius of C (and the base of each triangle in 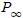 is very, very small... infinitely small!). is very, very small... infinitely small!). |
SO: area of C = area of 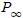
 , when n = ∞
, when n = ∞
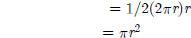
Problems
|
(1) What does it mean to multiply by an infinitely
small amount ( n = ∞)? (Can’t be same as multiplying by 0!) (2) What is a polygon with infinitely many infinitely small sides? (3) As n goes to infinity, |
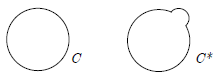 What
does it mean to say C is what |
Archimedes’ Solution
Proved 2 claims:
Claim I: There is a regular polygon as close in area to C as you care to
specify.
|
i.e., For any arbitrary small area ε, there is always
a number n such that
|
||
| in area from C by less than ε.) |
 |
not true for C* |
Consequence: The area of C is at most πr2.
Claim II: The area of C is at least πr2.
Consequence of I and II: The area of C is exactly πr2
Significance of Archimedes’ Solution: No mention of infinity!
III. Aristotle
 |
only world there is for Aristotle |
|
| Empiricist: Platonic Forms are in the physical world. |
|
Relevant Question: Is anything in nature infinite? Aristotle’s Answer:
actual infinite: that whose infinitude
exists at some point in time Note: For A., this is literally the distinction: Time is infinite, but not space |
 |
Aristotle’s Response to Zeno’s Paradoxes:
Achilles and the Tortoise
The distance between Achilles and the Tortoise is only potentially infinitely
divisible; it is not
actually infinitely divisible. And there is no contradiction in claiming that a
finite length is
potentially infinitely divisible.
or:
To travel a potentially infinitely divisible distance, Achilles needs a
potentially infinite time. And
there is nothing wrong in claiming he has such a time available.
Aristotle’s infinite: “the untraversible”
Something is infinite if, taking it quantity by
quantity, we can always take something outside.”
“It is not what has no part outside it that is infinite,
but what always has some part outside it.”
Under Moore’s reading, Aristotle rejects the “metaphysically infinite” and
adopts the “mathematically infinite”.
| Problem for Aristotle: What about the infinite past? | ||
 |
Already traversed? So actually infinite? |
|
Wittgenstein’s Story:
Suppose we come across a man saying “... 5, 1, 4, 3.”, who then proceeds to tell
us that he has just finished reciting π backwards for all past eternity. Why
does
this strike us as impossible, whereas someone who just starts reciting π
forwards
and will continue for all future eternity does not (given that we concede the
possibility of living forever).


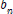 = base of triangle
= base of triangle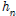 = height of triangle
= height of triangle