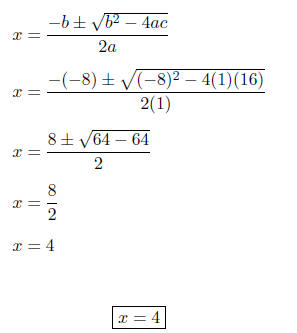THE QUADRATIC FORMULA
Definition:
• Quadratic Equation: is an equation that can be written in the form
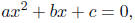
where a, b, and c are real numbers, a ≠ 0.
Important Properties:
• Quadratic Formula: The solutions of ax^2 + bx + c = 0 where a ≠ 0 are given by
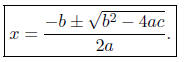
• The quadratic formula is a result of solving ax^2 + bx + c = 0 by
completing the square.
• The quadratic formula can be used to solve any quadratic equation.
• If b^2 - 4ac < 0 then there are no real solutions to the quadratic equation.
• If b^2 - 4ac = 0, then the quadratic equation has only one real zero.
• If b^2 - 4ac > 0, then the quadratic equation has two real solutions
Common Mistakes to Avoid:
• Before identifying a, b, and c to be used in the quadratic formula, make
sure one side of your equation
is zero.
• In the quadratic formula, the -b is also divided by 2a.
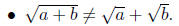
• Be careful when simplifying your final answer. Remember that
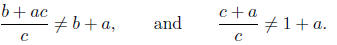
• The quadratic formula can only be used on a quadratic equation. Do not use
on a quadratic-type
equation without a change of variables.
PROBLEMS
Solve the following equations using the quadratic formula.
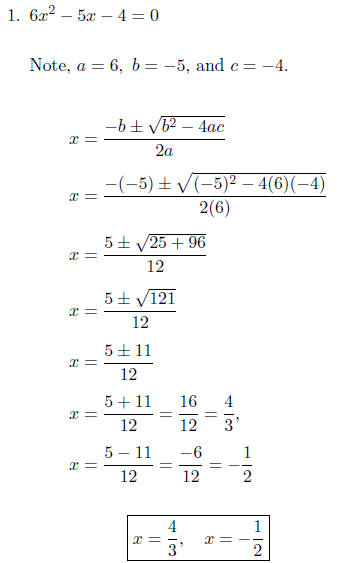
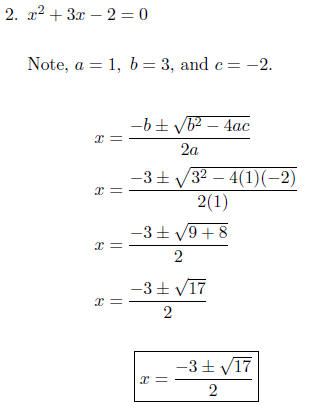
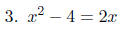
We must make one side zero before we can
identify a, b, and c.
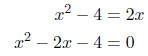
Therefore, a = 1, b = -2, and c = -4.
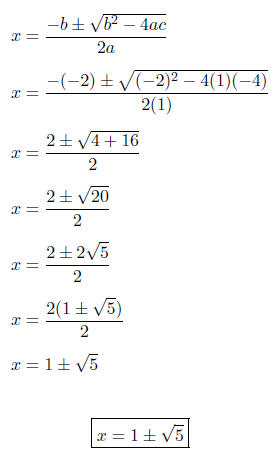
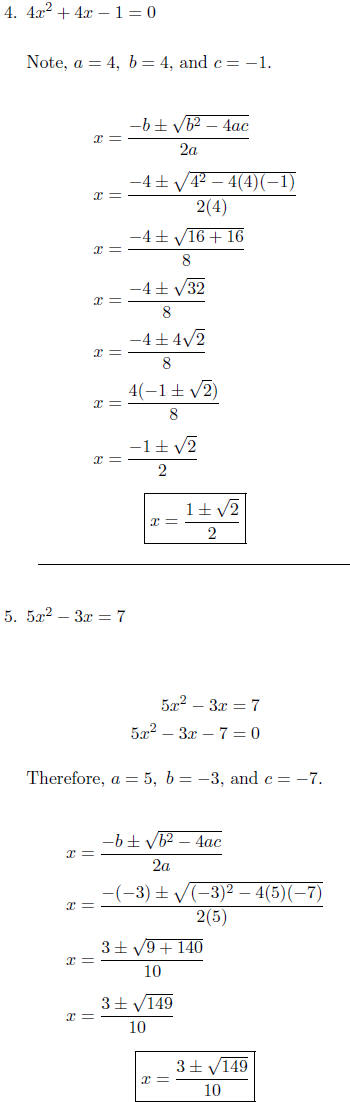
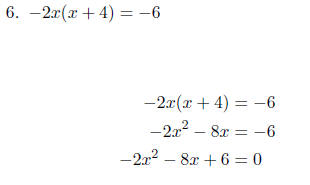
Note, that a -2 can be divided out of each
term. Therefore, before using the quadratic
formula, we will divide each term by -2.
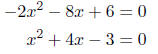
Hence, a = 1, b = 4, and c = -3.
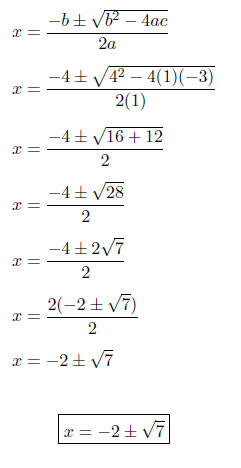
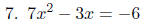
We must first make one side zero before identifying a, b, and c.
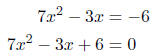
Therefore, a = 7, b = -3, and c = 6.
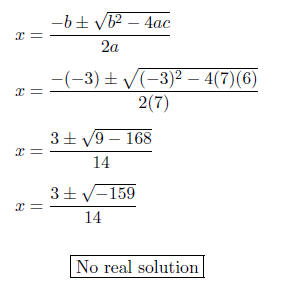
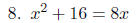
Once again, we must have one side zero be-
fore we can identify a, b, or c.
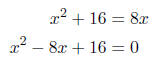
Therefore, a = 1, b = -8, and c = 16.