SYSTEMS OF LINEAR EQUATIONS - TI 83 METHOD

Before we really go over this method very much, we need to point out two differences in the calculators.
This pertains to how we go into the "Matrix" menu:

TI-83 Plus "2nd" button " x−1 " button This will bring up the "Matrix" menu. As always, when you are done: "2nd" button "mode" button will exit you out.

TI-83 "Matrx" button This will bring up the "Matrix" menu. As always, when you are done: "2nd" button "mode" button will exit you out.

This is best show by example:

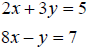
We are going to enter this into the calculator looking this way:

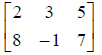
(this is actually called a matrix, you don't need to know that to solve these).
Its size is 2 rows by 3 columns
To solve this system of equations:
Step 1: Enter the Matrix into the calculator
Go into the "Matrix" menu (see above box):

You may or may not have numbers next to A, B, C, etc… Don't worry about it.
Right arrow to "Edit"

Notice that 1: [A] is highlighted, we are always going to put the matrix into A so just "enter" now:

You may or may not have numbers already here. Don't worry about it, as we type in our new numbers,
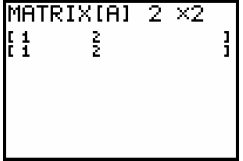
these get overwritten. We are going to enter how many rows, so we will type 2 and press "enter":

Now we are going to press in how many columns we have, so we will type 3 and press "enter":

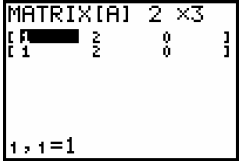
We will always enter "2 x3" when working with systems of linear equations in two variables. Now lets
recall the matrix from above:

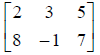
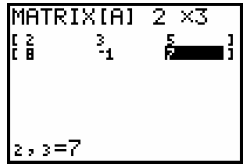
We notice that our highlighting is on the first entry. We are going to type in these numbers hitting "enter"
after each one. Don't worry about going down to the 2nd row, it will handle it automatically:

If you mess up entering the numbers, don't worry about it. Use the arrow keys to go to the one you want to
change and enter the new number and "enter" button. After you do the "enter" button on each number, it
saves it.

VERY IMPORTANT: now that we have it entered, lets exit out using "2nd" button and then "mode"
button.

Step 2:
Go back into "Matrix" menu (see box at the beginning of the document):

Step 3:
Right arrow to "Math":

Step 4:
Down arrow until "RREF" is highlighted:

and press "enter" button:

Step 5:
Go back into "Matrix" menu (again see beginning box for instructions on this):

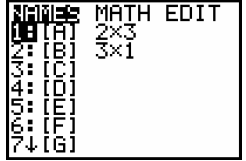
Notice "1: [A]" is already highlighted (which is good because that is where we entered our matrix in step
1); just press "enter" on it:

Put a closing parenthesis on this (not necessary just good practice to get into):

and press "enter" button:

The number circled in red will always be your x-value and the number circled in blue will always be your
y-value (they won't always be the same).

Step 6 (Optional).
If you ended up with decimals in step 5, you need to do the following steps to convert it to fraction:

"math" button
"enter" button
"enter" button

Do this step immediately after step 5 (it will still be in memory).

NOTES:
1. If you have fractions in your system of equations to begin with:

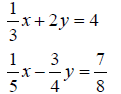
You will enter these into the matrix the same way. for the 1/3x, you would just enter :
1
"divide" button
3
"enter" button

2. If you end up with something like this on your display after you perform the RREF:

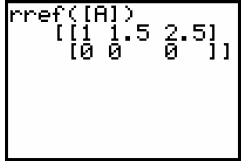
Notice the last line is always zeros. This means they are the same line and it is a "dependent equation" and
you will need to use the “c” substitution process.

3. If you end up with something like this on your display after you perform the RREF:

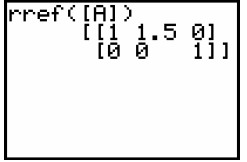
You will always have a [ 0 0 1], this means they are inconsistent systems or no solution problems.