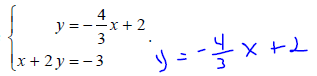MATH 237 LINEAR ALGEBRA

Definition

A solution to a system of two linear equations with two unknowns is an ordered pair that makes each of
the equations true.

Examples

Decide whether or not the given ordered pairs are solutions to the system of equations:

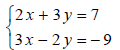
Is (5,−1) a solution to the system?

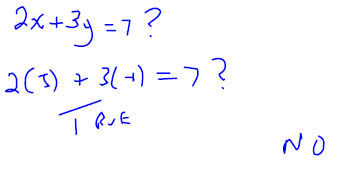
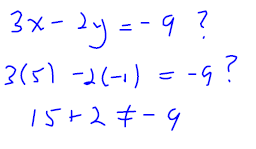
Is (−1,3) a solution to the system?

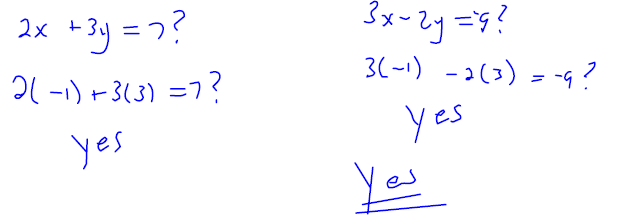
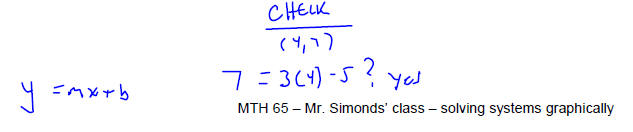
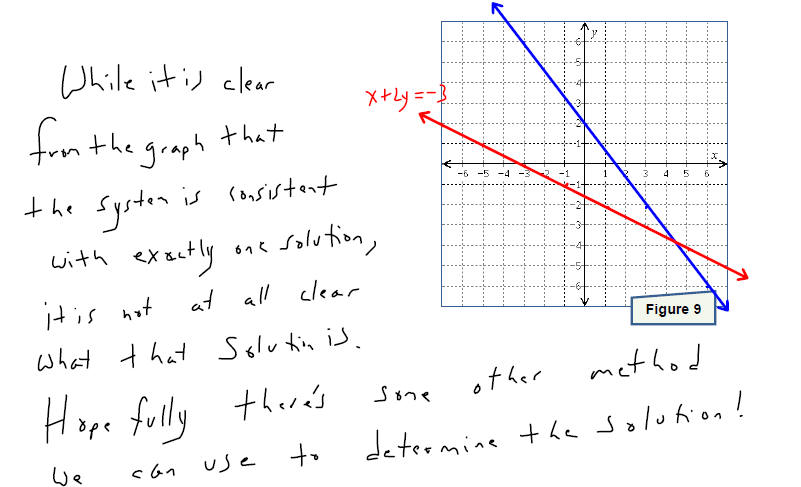
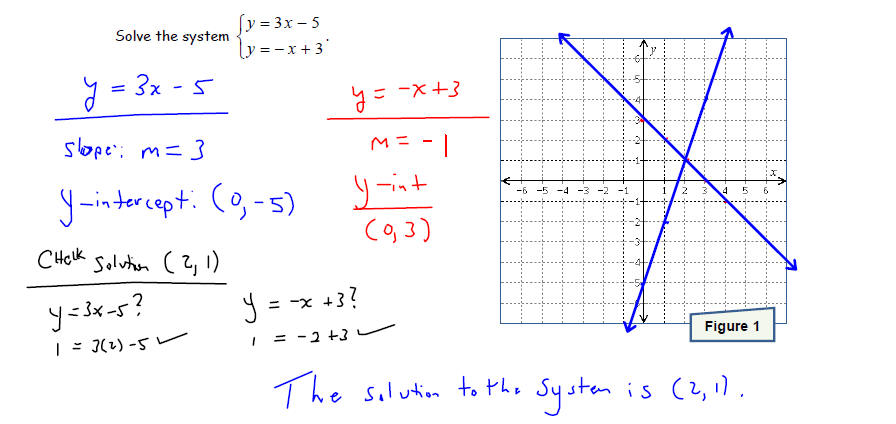
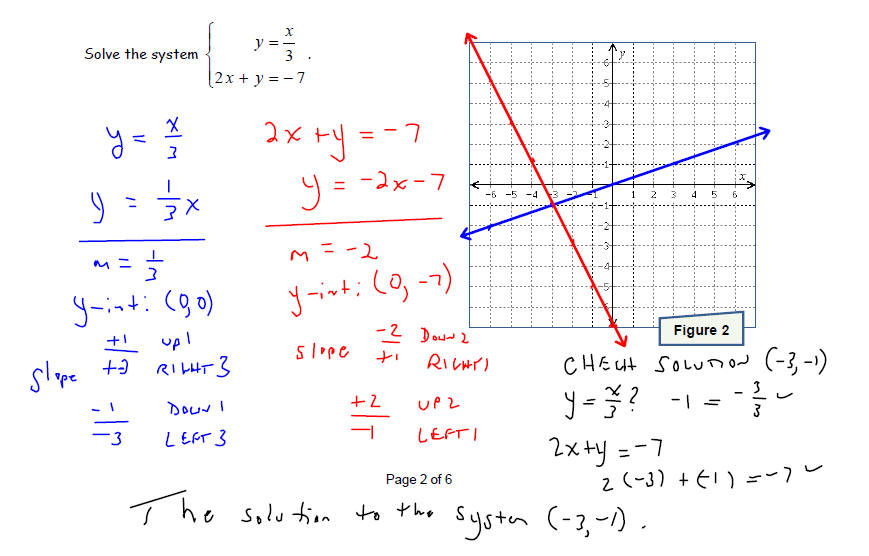
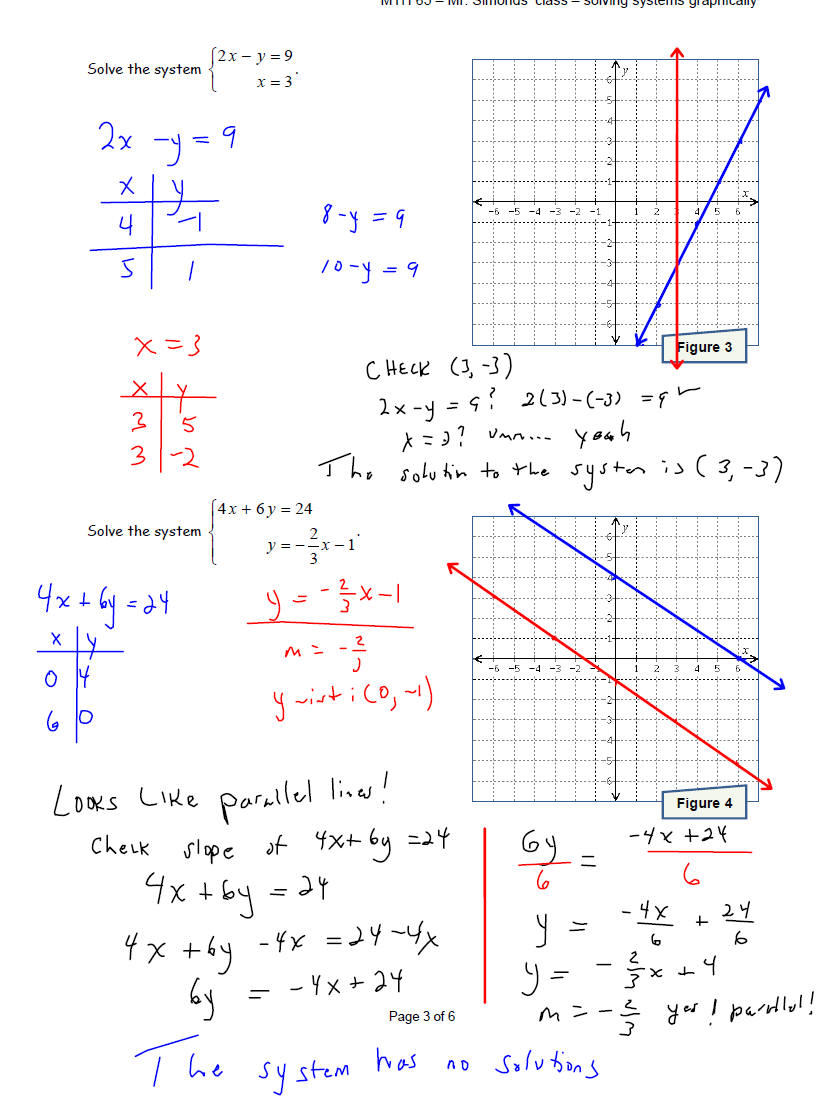
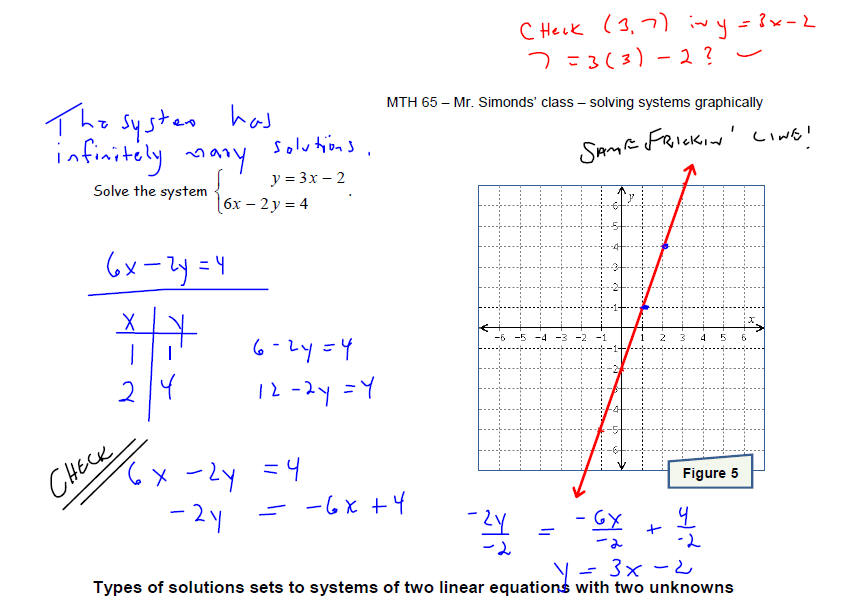
Solve each system of equations by graphing the two linear equations and finding the point(s) they
have in common. Make sure that you check your solution before stating your conclusion.

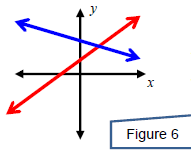
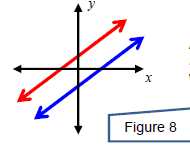
A system can have exactly one solution. In this case, the system is called
consistent and the equations are called independent. This happens
x when the two equations graph to lines that intersect at a single point.

A system can have an “infinite number” of solutions. In this case, the
system is called consistent and the equations are called dependent.
x This happens when the two equations graph to the same line

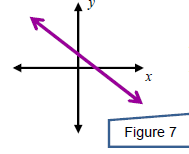
A system can have no solution. In this case, the system is called
inconsistent and the equations are called independent. This happens
x when the two equations graph to parallel lines.

Examples

For each system, write both equations in slope-intercept form and decide – without graphing –
whether the system is consistent or inconsistent and whether the equations are dependent or

Find the solution to the system of equations