Number Theory Homework 4 Solution

1. Given three integers a, b, c with c > 0, prove that lcm(ac, bc) = c · lcm(a, b).
Solution:

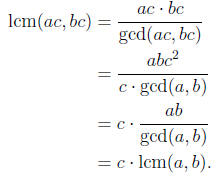
2. Use the Euclidean algorithm to compute lcm(357,−629, 221).
Solution: Since lcm(357,−629, 221) = lcm(lcm(357,−629), 221), we’ll first compute
lcm(357,−629) = lcm(357, 629). Using the Euclidean algorithm,

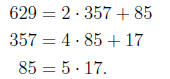
So gcd(357, 629) = 17, and thus lcm(357, 629) = 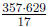= 13209. Next, we calculate
lcm(13209, 221). Again, using the Euclidean algoirthm,

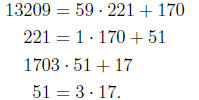
Therefore, gcd(13209, 221) = 17, and hence lcm(13209, 221) = 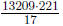= 171717

3. For any integer n, show that lcm(9n + 8, 6n + 5) = 54n^2 + 93n + 40.
Solution: For any integer n, we can write 1 = 2(9n + 8) − 3(6n + 5). This tells us
gcd(9n + 8, 6n + 5) = 1. So

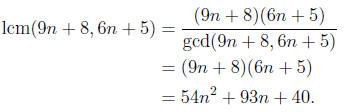
4. (a) Use the Fundamental Theorem of Arithmetic to prove that gcd(aⁿ, bⁿ) = (gcd(a, b))ⁿ for
any positive integer n. If particular, if a and b are relatively prime, then so are aⁿ and
bⁿ.

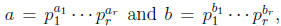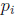Proof. By TFA, we can write where are distinct
primes and 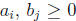. Let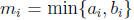 for all i. Then 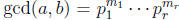, and
so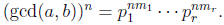

On the other hand,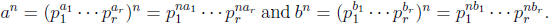
Note that for each i, 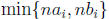= = 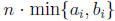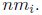Therefore,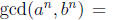

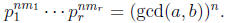
(b) If 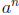divides 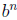, must a divide b? Explain your answer.
Solution: Yes. If 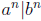, then 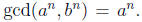From part (a), we know =
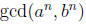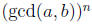. Combining, we get gcd(a, b) = a, and therefore a|b.

5. Without using the Euclidean algorithm, find the greatest common divisor and least common
multiple of a = 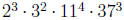and b =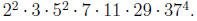. You may leave your answer
in factored form.

Solution: gcd(a, b) = 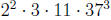and lcm(a, b) =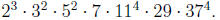

6. Without quoting Dirichlet’s Theorem, prove that there are infinitely many primes of the form
6k − 1.

Proof. First note that by the division algorithm, every odd prime greater than 3 is of the
form 6k + 1 or 6k + 5. Since 6k + 5 = 6(k + 1) − 1, it is true that every odd prime is of the
form 6k + 1 or 6k − 1.

Now suppose that there are finitely many primes of the form 6k−1, say 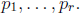Consider
the number N = 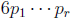− 1. Since N is of the form 6k − 1 and 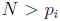for all i, N is an
odd composite integer and so must have prime factors of the form 6k + 1 or 6k − 1.

Note that the product of two numbers of the form 6k + 1 is again of that form. Thus, N
has a prime divisor of the form 6k −1, i.e. 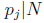for some j. But this means 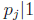, impossible.
Hence, there are infinitely many primes of the form 6k − 1.