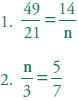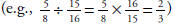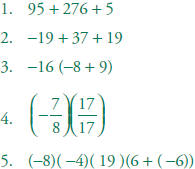Try the Free Math Solver or Scroll down to Tutorials!
 

 

 

 

 

 

 

 
 
 
 
 
 
 
 
 

 

 

 
 
 
 
 
 
 
 
 

Please use this form if you would like
to have this math solver on your website,
free of charge.

The California Mathematics Content Standards

Grade Six Mathematics Content Standards

By the end of grade six, students have mastered the four arithmetic operations with whole
numbers, positive fractions, positive decimals, and positive and negative integers; they
accurately compute and solve problems. They apply their knowledge to statistics and
probability. Students understand the concepts of mean, median, and mode of data sets
and how to calculate the range. They analyze data and sampling processes for possible bias
and misleading conclusions; they use addition and multiplication of fractions routinely to
calculate the probabilities for compound events. Students conceptually understand and
work with ratios and proportions; they compute percentages (e.g., tax, tips, interest).
Students know about π and the formulas for the circumference and area of a circle. They
use letters for numbers in formulas involving geometric shapes and in ratios to represent an
unknown part of an expression. They solve one-step linear equations.

  Number Sense

Students compare and order positive and negative fractions, decimals, and
mixed numbers. Students solve problems involving fractions, ratios, proportions,
and percentages:

Compare and order positive and negative fractions, decimals, and mixed
numbers and place them on a number line.

Interpret and use ratios in different contexts (e.g., batting averages, miles per
hour) to show the relative sizes of two quantities, using appropriate notations
(a/b, a to b, a:b).

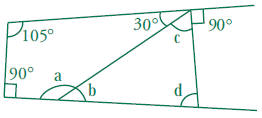
Write the following as ratios:

1. The ratio of tricycles to tricycle wheels

2. The ratio of hands to fingers

3. If there are 6 tricycle wheels, how many tricycles are there?

4. If there are 45 fingers, how many hands are there?

Use proportions to solve problems (e.g., determine the value of N if
4/7 = N/21, find the length of a side of a polygon similar to a known
polygon). Use cross-multiplication as a method for solving such problems,
understanding it as the multiplication of both sides of an equation by a
multiplicative inverse.

Find n if:

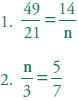
(This problem also applies to Algebra and Functions Standard 1.1.)

Calculate given percentages of quantities and solve problems involving
discounts at sales, interest earned, and tips.

Students calculate and solve problems involving addition, subtraction,
multiplication, and division:

2.1 Solve problems involving addition, subtraction, multiplication, and division
of positive fractions and explain why a particular operation was used for a
given situation.

2.2 Explain the meaning of multiplication and division of positive fractions and
perform the calculations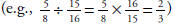

1. If 11/7 is divided by a certain fraction a/b, the result is 3/8. What is a/b?

2. Draw a rectangle that has a perimeter of 1 and an area of less than 1/30.

Solve addition, subtraction, multiplication, and division problems, including
those arising in concrete situations, that use positive and negative integers
and combinations of these operations.

Simplify to make the calculation as simple as possible and identify the
properties you used at each step:

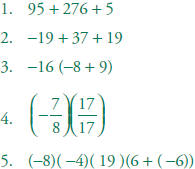
Determine the least common multiple and the greatest common divisor of
whole numbers; use them to solve problems with fractions (e.g., to find a
common denominator to add two fractions or to find the reduced form for a
fraction).
 

 Note: The sample
problems illustrate
the standards and
are written to help
clarify them. Some
problems are written
in a form that can be
used directly with
students; others will
need to be modified,
particularly in the
primary grades,
before they are
used with students.

The symbol
identifies the key
standards for
grade six.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 
 
Algebra and Functions

1.0 Students write verbal expressions and sentences as algebraic expressions and
equations; they evaluate algebraic expressions, solve simple linear equations,
and graph and interpret their results:

Write and solve one-step linear equations in one variable.

6y - 2 = 10. What is y?

1.2 Write and evaluate an algebraic expression for a given situation, using up to
three variables.

Joe’s sister Mary is twice as old as he is. Mary is 16. How old is Joe?

1.3 Apply algebraic order of operations and the commutative, associative, and
distributive properties to evaluate expressions; and justify each step in the
process.

1.4 Solve problems manually by using the correct order of operations or by using
a scientific calculator.

2.0 Students analyze and use tables, graphs, and rules to solve problems involving
rates and proportions:

2.1 Convert one unit of measurement to another (e.g., from feet to miles, from
centimeters to inches).

Suppose that one British pound is worth $1.50. In London a magazine costs
3 pounds. In San Francisco the same magazine costs $4.25. In which city is
the magazine cheaper?

When temperature is measured in both Celsius (C) and Fahrenheit (F),
it is known that they are related by the following formula:
9 × C = (F - 32) × 5.

What is 50 degrees Fahrenheit in Celsius? (Note the explicit use of
parentheses.)

Demonstrate an understanding that rate is a measure of one quantity per
unit value of another quantity.

Joe can type 9 words in 8 seconds. At this rate, how many words can he type
in 2 minutes?

2.3 Solve problems involving rates, average speed, distance, and time.

Marcus took a train from San Francisco to San Jose, a distance of
54 miles. The train took 45 minutes for the trip. What was the average
speed of the train?

3.0 Students investigate geometric patterns and describe them algebraically:

3.1 Use variables in expressions describing geometric quantities
(e.g., P = 2w + 2l, A = 1/2 bh, C =π d—the formulas for the perimeter
of a rectangle, the area of a triangle, and the circumference of a
circle, respectively).

A rectangle has width w. Its length is one more than 3 times its width. Find
the perimeter of the rectangle. (Your answer will be expressed in terms of w.)

3.2 Express in symbolic form simple relationships arising from geometry.
 

  
 
Measurement and Geometry

1.0 Students deepen their understanding of the measurement of plane and solid
shapes and use this understanding to solve problems:

Understand the concept of a constant such as π; know the formulas for the
circumference and area of a circle.

1.2 Know common estimates of π (3.14; 22/7) and use these values to estimate
and calculate the circumference and the area of circles; compare with actual
measurements.

1.3 Know and use the formulas for the volume of triangular prisms and cylinders
(area of base × height); compare these formulas and explain the similarity
between them and the formula for the volume of a rectangular solid.

Find the volumes (dimensions are in cm).


 

  
 
2.0 Students identify and describe the properties of two-dimensional figures:

2.1 Identify angles as vertical, adjacent, complementary, or supplementary and
provide descriptions of these terms.

Use the properties of complementary and supplementary angles and the sum
of the angles of a triangle to solve problems involving an unknown angle.

Find the missing angles.

2.3 Draw quadrilaterals and triangles from given information about them (e.g., a
quadrilateral having equal sides but no right angles, a right isosceles triangle).
 

  
 
Statistics, Data Analysis, and Probability

1.0 Students compute and analyze statistical measurements for data sets:

1.1 Compute the range, mean, median, and mode of data sets.

1.2 Understand how additional data added to data sets may affect these computations
of measures of central tendency.

1.3 Understand how the inclusion or exclusion of outliers affects measures of
central tendency.

1.4 Know why a specific measure of central tendency (mean, median, mode)
provides the most useful information in a given context.

2.0 Students use data samples of a population and describe the characteristics
and limitations of the samples:

2.1 Compare different samples of a population with the data from the entire
population and identify a situation in which it makes sense to use a sample.

Identify different ways of selecting a sample (e.g., convenience sampling,
responses to a survey, random sampling) and which method makes a sample
more representative for a population.

Analyze data displays and explain why the way in which the question was
asked might have influenced the results obtained and why the way in which
the results were displayed might have influenced the conclusions reached.

Identify data that represent sampling errors and explain why the sample (and
the display) might be biased.

Identify claims based on statistical data and, in simple cases, evaluate the
validity of the claims.

3.0 Students determine theoretical and experimental probabilities and use these
to make predictions about events:

Represent all possible outcomes for compound events in an organized way
(e.g., tables, grids, tree diagrams) and express the theoretical probability of
each outcome.

3.2 Use data to estimate the probability of future events (e.g., batting averages or
number of accidents per mile driven).

Represent probabilities as ratios, proportions, decimals between 0 and 1, and
percentages between 0 and 100 and verify that the probabilities computed
are reasonable; know that if P is the probability of an event, 1-P is the
probability of an event not occurring.

3.4 Understand that the probability of either of two disjoint events occurring is
the sum of the two individual probabilities and that the probability of one
event following another, in independent trials, is the product of the two
probabilities.

Understand the difference between independent and dependent events.
 

  
 
Mathematical Reasoning

1.0 Students make decisions about how to approach problems:

1.1 Analyze problems by identifying relationships, distinguishing relevant from
irrelevant information, identifying missing information, sequencing and
prioritizing information, and observing patterns.

1.2 Formulate and justify mathematical conjectures based on a general description
of the mathematical question or problem posed.

1.3 Determine when and how to break a problem into simpler parts.

2.0 Students use strategies, skills, and concepts in finding solutions:

2.1 Use estimation to verify the reasonableness of calculated results.

2.2 Apply strategies and results from simpler problems to more complex
problems.

2.3 Estimate unknown quantities graphically and solve for them by using
logical reasoning and arithmetic and algebraic techniques.

2.4 Use a variety of methods, such as words, numbers, symbols, charts, graphs,
tables, diagrams, and models, to explain mathematical reasoning.

2.5 Express the solution clearly and logically by using the appropriate mathematical
notation and terms and clear language; support solutions with
evidence in both verbal and symbolic work.

2.6 Indicate the relative advantages of exact and approximate solutions to
problems and give answers to a specified degree of accuracy.

2.7 Make precise calculations and check the validity of the results from the
context of the problem.

3.0 Students move beyond a particular problem by generalizing to other
situations:

3.1 Evaluate the reasonableness of the solution in the context of the original
situation.

3.2 Note the method of deriving the solution and demonstrate a conceptual
understanding of the derivation by solving similar problems.

3.3 Develop generalizations of the results obtained and the strategies used and
apply them in new problem situations.