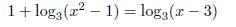Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Math 111 Final Exam Review

Chapter 5

5.1: Radicals and Rational Exponents

You should have your exponent laws imprinted in your gray matter. You should be comfortable with
reducing radical and exponential expressions.

41. Simplify the expression

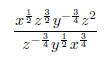
42. True/False?

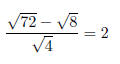
5.2: Exponential Equations and 5.2A: Compound Interest and the numbere

You need to be comfortable working with exponential equations. You need to be able to set up
exponential equations from word problems. You need to be able to solve for variables in the exponent
using logarithms. You should know the formulas for compound interest.

Problems from 5.2: 19-23, 51-62, 64-76.

Problems from 5.2A: 1-29.

43. Hercules ate 7 grams of Uranium, and now he is sprouting eyes at an exponential rate. He had two eyes
when he ate the Uranium. 3 hours later, Hercules has 14 eyes. Find an exponential function whose
input is the number of hours since Hercules ingested Uranium, and the output is the number of eyes
Hercules has. How many eyes will Hercules have after 24 hours? When will Hercules have 5000 eyes?
Give an exact answer and decimal approximation.

44. Recall the formula for continuous compounding is f(t) = Pe^rt. You invest 500$ in an account with
7.5% interest, compounded continuously. How much will be in your account after 5 years? How long
will it take for your account to double? Give an exact answer and decimal approximation.

5.3: Common and Natural Logarithms

You should know the properties of Logarithms in general. Namely, they are the inverse functions to
exponential functions, their domain and range...all the information in the box on p. 365.

Problems from 5.3: 1-36, 43-46, 84

5.4: Properties of Logarithms and 5.4A: Logarithmic Functions to Other Bases.

You need to be very comfortable with the Product Law, Quotient Law, and Power Law. These are the
main tools for working with logarithms. You should be able to write sums and differences of logarithms
as a single logarithm.

Problems from 5.4: 1-31.

Problems from 5.4A: 1-60, 69 - 74

45. True/False.

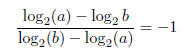
for a, b > 0, a≠b.

46. Write the following as a single logarithm.

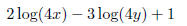
5.5:Algebraic Solutions of Exponential and Logarithmic Equations

You should be able to solve exponential and logarithmic equations algebraically. Don’t forget to check
your answers when solving logarithmic equations.

Problems from 5.5: 1-29, 35- 80.

47. Solve the following equation:

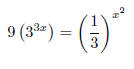
48. Solve the following equation:

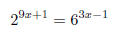
49. Solve the following equation.

Algebra Solutions

Free math tutorials and more...