RECURRENCES AND GENERATING FUNCTIONS

The Rules. There are too many problems to consider. Pick a few problems that
you find fun, and play around with them. The only rule is that you may not pick
a problem that you already know how to solve: where’s the fun in that?

General problem solving strategies. Try small cases; plug in smaller numbers.
Search for a pattern. Draw pictures. Choose effective notation. Work in groups.
Divide into cases. Look for symmetry. Work backwards. Argue by contradiction.
Parity? Pigeonhole? Induction? Generalize the problem, sometimes that makes it
easier. Be flexible: consider many possible approaches before committing to one.
Be stubborn: don’t give up if your approach doesn’t work in five minutes. Ask.
Eat pizza, have fun!

1. (Larson 5.4.12) Let p and q be real numbers with 1/p−1/q = 1, and 0 < p≤ 1/2.
Show that



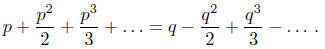
2. (Johann Bernoulli, 1697(!)) Prove that



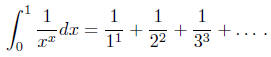
3. (Larson 5.2.15) Prove that



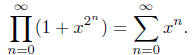
Interpret this statement.

4. (1992: B2) For non-negative integers n and k define Q(n, k) to be the coefficient
of x^k in the expansion of (1 + x + x² + x³)ⁿ. Prove that


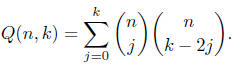
5. Show that the number of partitions of n into parts that are not divisible by 3
equals the number of partitions of n in which no part appears more than twice.

6. (1989: B3) Let f be a function on [0,∞) differentiable, and satisfying f'(x) =
−3f(x) + 6f(2x) for all x > 0. Assume that 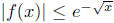for all x (so that f(x)
tends rapidly to 0 as x increases). For n a non-negative integer, define

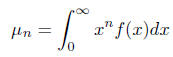
(sometimes called the n-th moment of f). a) Express μn in terms of μ₀. b) Prove
that the sequence 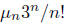always converges, and that the limit is zero if and only
if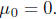

7. Evaluate


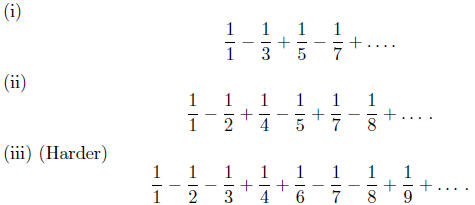
Dirichlet figured out how to generalize these to infinitely many such formulae,
and these are in fact useful in showing that there are infinitely many primes in
arithmetic progressions.

8. Find a closed formula for



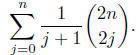
9. (Larson 5.4.20) Let B(n) denote the number of ones in the binary expansion of
the positive integer n. Determine whether or not


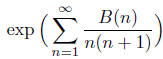
is a rational number.

10. (Zeitz 4.3.22) Alberto places N checkers in a circle, some of which are black
and the others white. Bet¨ul places new checkers in between the pairs of adjacent
checkers in Alberto’s ring: she places a white checker between every two of the
same color, and a black checker between every pair of opposite color. She then
removes Alberto’s original checkers leaving a new ring of N checkers. Alberto now
performs the same operation on this ring of checkers, and so on. Prove that if N
is a power of 2 then all the checkers will eventually be white, no matter what the
initial configuration.