Mathematics Transition Guide

B Essential Skills & Competencies For
General Entry Points of Regent University Mathematics

1. Skills and competencies for Entering Pre-Calculus (Algebra/Trigonometry)*

A) Arithmetic
Fluency in real number arithmetic-PEMDAS, fraction arithmetic,
rational roots of whole numbers, rules of exponents,
simplification of rational number expressions, including
those with fractional exponents in numerators or denominators.
Basic understanding of complex numbers.

B) Algebra
Ability to translate basic word problems involving one or
several unknowns into problems of finding solutions to one
or several equations (or inequalities) each with one or several
variables representing those unknowns. Ability to recognize
reasonableness or un-reasonableness of candidate
solutions. Types of problems may involve proportionality-similarity,
area-length measurements, volumes-surface area
measurements, etc.

C) Algebra
Facility with expressions involving variables such as
polynomials, including the ability to understand meaning
of roots and the ability to determine if a given number is a
root of a given polynomial; factorization, ability to describe
and compute all attributes of linear expressions in one variable
(m*x+b), factor quadratics using the coefficients of the
quadratic and the quadratic formula, recognition of complex
roots as roots of quadratics; ability to find factorizations of
higher-order polynomials with additional information (e.g.
factoring out a common power of the variable, or given a root
and polynomial division). Facility with rational expressions
involving one or several variables (e.g. simplifying a rational
expression including one or several variables, including those
with rational exponents in numerators and denominators).

D) Algebra
Facility with concepts related to functions-single-valued-ness,
algebraic formulae such as f(x) = 2x³ + 7, tabular and
x-y coordinate plane representations of functions and their
graphs, the vertical line test, and meanings of domains and
ranges. The basic function families: polynomial, exponential
and logarithmic, rational and periodic (cf. trigonometry).
Understanding the relationship between a function f(x) and
functions such as f(x)+k, f(x+h), a* f(x), f(a*x), etc. In general,
the elementary analysis of the numerical, functional and
graphical attributes of functions (polynomial, exponential,
logarithmic) is a central topic.

E) Trigonometry
Basic notions of triangle components-angles, side
lengths, right triangle attributes. Similarity and congruence
of triangles. Definitions of the six elementary trigonometric
functions: sine, cosine, etc. via triangle ratios (SOHCAHTOA) and
unit circle coordinate definitions. Basic trig identities such
as the Pythagorean, addition, and subtraction identities,
and the ability to retrieve such information quickly. Use of
such trigonometry in basic geometric and/or story problems
involving proportionality, triangles, etc. Such problems may
include but are not limited to computing measurements of
inaccessible objects such as tall trees and buildings using
measurable objects.

*Not an entry point math course option at ISU

2. Skills and competencies for Entering Calculus i

A) Algebraic Functions
Experiences with functions, including analysis of families
of functions (linear, quadratic, general polynomial, exponential,
trigonometric, rational, logarithmic, and piecewise).
Analysis of these functions should include: zeros, maxima
and minima, domain and range, global and local behavior,
intercepts, and asymptotes. Ability to recognize, represent,
transform, compose, and find inverses of functions, and to
represent functions in multiple ways: via algebraic formulae,
graphs, data tables, and descriptions such as “the volume of
a cylinder of fixed height is proportional to the square of its
radius”, and ability to go back and forth between these representations.
Understand and analyze relations that are not
functions such as x² + y² = 5 and x = y².

B) Algebraic Equations and Inequalities
Solve inequalities and equations using algebraic and
graphic methods, including equations involving exponents
and logarithms, and equations of quadratic form such as
e^2x - 3e^x + 2 = 0. Solve systems of equations, including
inconsistent and dependent systems. Be able to represent
systems of two equations and two unknowns geometrically.

C) Algebraic Expressions
Ability to meaningfully manipulate algebraic expressions
to get equivalent forms by simplifying, factoring, expanding,
composing, decomposing, using order of operations, using
laws of exponents and logarithms and applying properties of
real numbers. Understand the difference between equations
and expressions.

D) Rate of Change
Familiarity with such examples as the speed of a car, the
number of people per year by which a population increases,
and slope of a line. Ability to analyze average and instantaneous
rate of change in multiple ways including: numeric, algebraic,
and graphic representations. Students should distinguish
between a constant rate of change and a non-constant rate
of change. They should be thoroughly comfortable with using
appropriate units for both functions and their rate of change.

E) Geometry and Trigonometry–Coordinates
Use (x,y) coordinates to describe points, lines, circles and
rectangles. Use formulas for distance, midpoint and slope,
and the Pythagorean Theorem, and have some degree of
understanding where they come from. Find and analyze
equations that represent lines, circles and parabolas. Familiarity
with the other conic sections–ellipses and hyperbolas.

F) Geometry
Find perimeter, area, volume and surface area of various
objects. Estimate these quantities as a check on accuracy. Recognize
and use appropriate units, and use dimensional analysis.

G) Trigonometry
Study right-triangle trigonometry and unit circle trigonometry.
Understand the trigonometric ratios, the Pythagorean
Theorem and its converse, and the special-case triangles:
30-60-90 and 45-45-90. Understand the trigonometric
functions including their domains, ranges and periodicity.
Understand the effect of various transformations on their
amplitudes and periodicity. Know basic identities such as
the Pythagorean, addition, and subtraction identities, and be
able to use the Law of Sines and Law of Cosines. Use trigonometry
to solve applied problems. Be able to solve simple
trigonometric equations with multiple solutions, such as
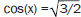and sin(x) = 0.6.

H) Theorems and Proofs
Ability to read and understand a simple proof or mathematical
argument, at the level given in a collegiate textbook.
Understand that a theorem does not imply its converse –
e.g. “Differentiability implies continuity” does not mean that
continuity implies differentiability. Ability to formulate and
test conjectures, and understand the difference between
noticing a pattern and proving that the pattern always holds.

 

3. Skills and competencies for Entering Calculus II

In addition to the material below, it is assumed that an incoming Calculus II student has mastered
all the material recommended for success in Calculus I, as listed above.

A) Limits and Continuity
Understand and be able to compute limits in graphic,
numeric and algebraic contexts. Understand continuity in
these contexts as well. Be familiar with the Intermediate
Value Theorem.

B) Derivatives
Definitions and Theorems: Understand the limit definition
of the derivative, the connection between differentiability
and continuity, the Mean Value Theorem, and Rolle’s
Theorem. Understand the derivative in terms of slope of a
tangent line, and an instantaneous rate of change
Computation: Be able to write the formula for f’ quickly
and accurately given a formula for a function f, either defined
by a formula or defined implicitly (this is the equivalent to
knowing one’s multiplication tables).
Geometry: Given a graph of a function f, be able to sketch
a graph of f’ that, while not necessarily perfect, should be
positive when f is increasing, negative when f is decreasing,
and flat when f has a local extremum. The intervals where f’
is increasing and decreasing should correspond to where f is
concave up or concave down.
Applications: Given a description of a function f, such
as “The height H of a column of mercury in a thermometer
is given by H=f(t), where t is the temperature in degrees
Fahrenheit,” be able to describe the meaning of f’, including
understanding its units. Ability to set up and solve global
optimization problems. Find exact values of local maxima,
local minima, and points of inflection of a function. Other
applications, such as Newton’s Method and L’Hopitals Rule
are desirable as well.

C) Integrals
Most Calculus II courses start with integrals, but many of
them assume a familiarity with antiderivatives from Calculus I.
Ideally, know how to find antiderivatives of basic functions,
and be familiar (if not fluent) with u-substitution. Understand
the meaning of the constant of integration. Understand the
definite integral as the limit of Riemann sums. Be able to
approximate the definite integral of a function over a given
interval with a calculator. Understand and be able to apply
the Fundamental Theorem of Calculus.

4. General skills & competencies for Entering Statistics

A) Algebra
Use and apply algebraic concepts that include ratio, proportion,
percentage, slope and intercept. Be able to transfer
algebra competencies to statistics applications.

B) Calculators and software
Have experience using calculators to solve algebraic equations.
Be familiar with (or ability to independently learn) software
such as jmp.

C) Modeling
Be able to do least squares regression and inference.

Engineering statistics Should be preceded by an introduction to calculus. Knowledge of functional notation, summation notation, facility with linear functions, and the ability to solve algebraic equations (e.g., quadratic equations) as part of a good working knowledge of high school algebra. Be familiar with exponential and logarithmic functions. Know basic techniques of integration and differentiation. Have exposure to exponential, Poisson, and normal distributions.

5. Skills & competencies for Entering Liberal Arts Math

Liberal Arts Mathematics covers a range of liberal arts mathematics courses. At the Regent universities, these courses include:
Iowa State University: Math 105 Introduction to Mathematical Ideas
University of Northern Iowa: 800:023 Math for Decision Making

A) Arithmetic
Fluency in real number arithmetic and fraction arithmetic,
rules of exponents, square roots. Knowing when it is appropriate
to multiply, divide, add, subtract or exponentiate.

B) Modeling
Ability to translate a verbal situation into a mathematical
problem, and to check the solution for reasonableness.

C) Algebra
Ability to solve linear equations and inequalities in one variable,
facility with linear equations and inequalities (slope of
a line, two-point form, point-slope form, slope-intercept form,
etc.), finding the intersection of two lines/the solution of two
linear equations in two unknowns.

D) Symbolic Manipulation
Facility with effectively working with symbolism. Be able
to distinguish between expressions like (P+Q’) and (P+Q)’ in
both reading and their writing.

E) Representation
The ability to use graphs, Venn-diagrams, pie charts, data-tables,
and other pictures that are used to represent mathematical
situations.

F) Generalization
The ability to generalize from examples, and then test
the generalization by applying it to additional situations.
Mathematics involves finding answers to specific questions
according to prescribed rules, but it also involves generalizing
from specific problems to general principles.

G) Independence
The ability to go beyond being told what to do at every step
and take the responsibility to understand the context of the
topics being discussed and to independently proceed using
appropriate methods to solve problems.

6. Skills & competencies for Entering Elementary Education Math

A) Overall
Positive disposition toward the study and learning of
mathematics. Belief that all children can learn mathematics.
Experience in the use of technology for learning
mathematics.

B) Number and Operations
Work flexibly with and understand the meaning and
effects of arithmetic operations with rational numbers,
their position in the real number system, and can use that
understanding to solve problems. Use properties of addition
and multiplication to simplify computations.

C) Algebra
Able to represent, analyze and generalize a variety of
patterns with tables, graphs, words and symbolic rules.
Possess a conceptual understanding of different uses of
variables, graphs and the nature of changes in quantities.

D) Geometry
Able to describe, classify and understand relationships
among two- and three-dimensional objects using their
defining properties. Can create and critique inductive and
deductive arguments concerning geometric ideas and relationships,
such as congruence, similarity and the Pythagorean
relationship.

E) Measurement
Understand relationships among the angles, side
lengths, perimeters, areas and volumes of similar objects.
Can select and use units of appropriate size and type
when working with such measures. Select and apply techniques
and tools for measuring.

F) Data Analysis and Probability
Can interpret measures of center and spread. Understand
the appropriate use and how to analyze histograms,
box plots, and scatter plots. Able to use observations
about differences between two or more samples to make
conjectures about the populations from which the samples
were taken. Command a basic understanding of probability
to make and test conjectures about the results of experiments
and the concept of randomness.