Quadratic Equations

Definition 1.1. A quadratic equation is an equation in the form

ax² + bx + c = 0,

where a, b, and c are real numbers, and a is nonzero. “a” is the coefficient of
the quadratic term (or, is the leading coefficient), “b” is the coefficient of
the linear term, and c is the constant term.

Remark 1.2. Officially, the only tool we have to use in solving quadratic equations
is factoring. There are some quadratics, however, that do not factor nicely,
or the factorization does not come to mind easily.

Definition 1.3. The method of solving a quadratic equation know as completing
the square involves transforming a quadratic into a perfect square.

Remark 1.4. Add picture here for geometric interpretation.

Item 1.5. We look for a pattern in the square of binomials:

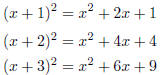
Notice that the linear term is twice the constant in the binomial we are squaring.
Moreover, notice that the constant term of the quadratic is the square of
the binomial’s constant. Therefore, when we complete the square, we want the
constant term to be the square of one-half the linear term.

Example 1.6. Solve the following quadratic by completing the square:

x² − 4x + 3 = 0.

Soln: In order to solve by completing the square, we wish to move the
constant term out of the way:

x² − 4x = −3.

Now, in our list above, we noticed that perfect squares have the constant term
as the square of half the middle term. Thus, we add it to both sides of the
equation:

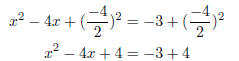
Again, from our list above, we see that the square quadratic factors as the square
of a sum of x and half the linear term:
(x − 2)^2 = 1

Solving for x, we take the square root of each side:

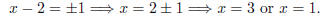
Example 1.7. Solve the following quadratic by completing the square:

x² − x − 1 = 0.

Soln: Following the same steps as above we have:

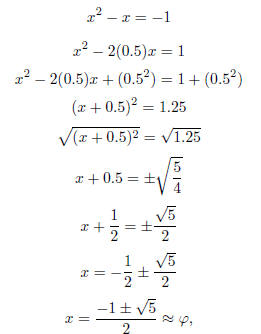
where 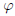is the Golden Ratio.

Remark 1.8. Completing the square will only work if the leading coefficient,
that is, the coefficient of the quadratic term, is one. What can we do if it is
not?

The Quadratic Formula Consider the general quadratic equation

ax² + bx + c = 0

We wish to complete the square, so we must have a leading coefficient of one.
Divide everything by “a”:

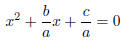
Clear the constant term as before:

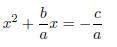
Again, we wish to have our new constant term the square of half the linear term:

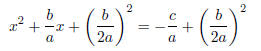
Simplifying the left side, and finding a common denominator for the right, we
have

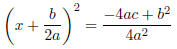
Taking the square root of each side gives

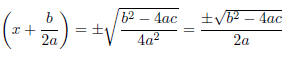
And solving for x:

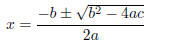
Definition 1.9. The quadratic formula is an algorithm by which to find the
roots of a quadratic equation. The two roots of an equation of the form

ax² + bx + c = 0

are

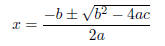
Example 1.10. Find the roots of the quadratic equation:

x² = 5 − 3x

Soln: First, we must put the equation in the correct form:

x² + 3x − 5 = 0.

Using the quadratic formula, with a = 1, b = 3, c = −5, we have:

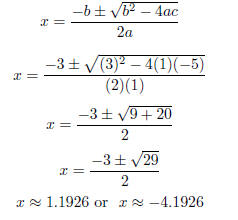
Definition 1.11. The discriminant is the term underneath the radical in the
quadratic formula, namely, b^2 − 4ac.

Remark 1.12. If the discriminant is positive, we will have two real roots. If the
discriminant is zero, we will have one real root. If the discriminant is negative,
we have no real roots.

Item 1.13. Please to eight of the following problems in section 3.1 for Friday:
1, 3, 5, 7, 13, 14, 27, 29, 37, 38, 47, 48, 55, 63, 65, 77

2 The Graph of a Quadratic Function

Remark 2.1. Since a quadratic is characterized by having an x² term, quadratics
can be shown to be reflections, translations, and stretches of the base function
y = x².

Example 2.2. Graph the quadratic function y = x² − 4x + 3.

Soln: By completing the square, we will be able to shift the graph of x² to
the graph of y :

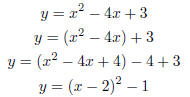
So our function is x² shifted two units to the right and one unit down. Notice
that the lowest point of x², (0, 0) is moved to (2,−1).

Definition 2.3. The turning point that occurs in a parabola, the graph of a
quadratic function, is called the vertex of the function. Since the base quadratic
is an even function, all quadratics have an axis of symmetry, the vertical line
passing through the vertex. If the parabola opens upwards, the vertex will be
the minimum of the function, and if it opens upwards, the vertex will be the
maximum.

Definition 2.4. A dilation or stretching of a quadratic will affect how widely
the parabola opens.

Example 2.5. Graph the function y = 3x² + 6x + 3.

Soln: Again, we’ll complete the square to see how the graph of x² moves:

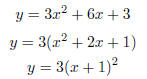
So x² is shifted one to the left and then “multiplied by three.” Notice that
points like (0, 3) and (2, 27) are on the graph of 3(x + 1)² instead of the points
(0, 1) and (2, 9) on the graph of (x₁)². Thus, the multiplying by three makes the
graph steeper, or skinner.

Remark 2.6. If a quadratic function is in the form

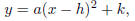
then the vertex of the graph is at (h, k) and the value of a characterizes how
“fat/skinny” the graph is: if a > 0, the graph opens upward. If a < 0, the graph
opens downwards. If |a| > 1, the graph gets skinner, and if |a| < 1, the graph
spreads out.

Example 2.7. Graph the function y = −2x² + 12x − 16.

Soln: Again, we complete the square. Remember that the leading coefficient
must be one for this to work:

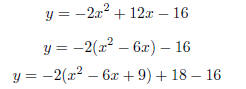
The “+18” balances out the “−2 · +9” inside the parentheses.

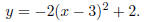
So the graph of y looks like the graph of x² moved three units to the right,
flipped over the x-axis, made skinner, and shifted vertically two units up.

Remark 2.8. Remember that the maximum or minimum of a quadratic always
occurs at the vertex. Since we are using complete the square, the vertex can also
be written as

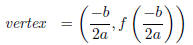
Example 2.9. We saw above that the vertex of y = −2x² + 12x − 16 is (3, 2).
We can get that directly by seeing that the vertex is at (−b/2a, f(−b/2a))

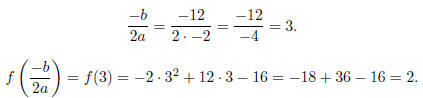
So the vertex of y is at (3, 2).

Item 2.10. The following homework problems are not assigned, but it is
highly recommended that you do them, for help on the test. For section
5.2, please do

1, 5, 7, 13, 19, 21, 23, 25, 27, 31, 33 − 38, 39, 41, 51.