Dividing Fractions
Explaining Why "Invert and Multiply" is Valid by Re-
lating Division to Multiplication
The procedure for dividing fractions is easy enough to carry out, but why is it
a valid method? Before we answer this question in general, consider a special
case. Recall that every whole number is equal to a fraction (for example,
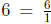 ). Therefore we can apply the "invert and
multiply" procedure to
). Therefore we can apply the "invert and
multiply" procedure to
whole numbers as well as to fractions. According to this procedure,
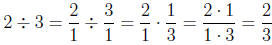
Notice that this result, that
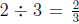 , agrees with our findings earlier in
, agrees with our findings earlier in
this chapter: that we can describe fractions in terms of division, namely that
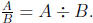
In general, why is the "invert and multiply" procedure a valid way to
divide fractions? One way to explain this is to relate fraction division to
fraction multiplication. Recall that every division problem is equivalent to a
multiplication problem (actually two multiplication problems):
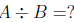
is equivalent to
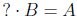
(or B · ? = A). So
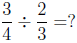
is equivalent to

Now remember that we want to explain why the "invert and
multiply" rule
for fraction division is valid. This rule says that
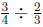 ought to be equal to
ought to be equal to
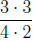
Let's check that this fraction works in the place of the ?
in Equation 1. In
other words, let's check that if we multiply
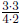 times
times
![]() , then we really do
get
, then we really do
get
![]() :
:
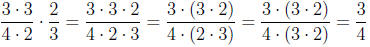
Therefore the answer we get from the "invert and multiply"
procedure really
is the answer to the original division problem
![]() . Notice that the
line
. Notice that the
line
of reasoning above applies in the same way when other fractions replace the
fractions
![]() and
and
![]() used above.
used above.
It will still be valuable to explore fraction division further, interpreting
fraction division directly rather than through multiplication.
Class Activity 0A: Explaining "Invert and Multiply" by
Relating Division to Multiplication
Using the "How Many Groups?" Interpretation to Ex-
plain Why "Invert And Multiply" Is Valid
Above, we explained why the "invert and multiply" procedure for dividing
fractions is valid by considering fraction division in terms of fraction
multiplication.
Now we will explain why the "invert and multiply" procedure is
valid by working with the "how many groups?" interpretation of division .
Consider the division problem
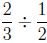
The following is a story problem for this division
problem:
How many
![]() cups of water are in
cups of water are in
![]() of a cup of water?
of a cup of water?
Or, said another way:
How many times will we need to pour
![]() cup of water into a
cup of water into a
container that holds
![]() cup of water in order to fill the container?
cup of water in order to fill the container?
From the diagram in Figure 1 we can say right away that the answer to this
problem is "one and a little more" because one half cup clearly fits in two
thirds of a cup, but then a little more is still needed to fill the two thirds
of
a cup. But what is this "little more"? Remember the original question: we
want to know how many
![]() cups of water are in
cups of water are in
![]() of a cup of water. So the
of a cup of water. So the
answer should be of the form "so and so many
![]() cups of water." This means
cups of water." This means
that we need to express this "little more" as a fraction of
![]() cup of water.
cup of water.
How can we do that? By subdividing both the
![]() and the
and the
![]() into common
into common
parts, namely by using common denominators.

Figure 1: How Many 1/2 Cups of Water Are in 2/3 Cup?
When we give
![]() and
and
![]() the common
denominator of 6, then, as on the
the common
denominator of 6, then, as on the
right of Figure 1, the
![]() cup of water is made out of 3 parts (3 sixths of a
cup of water is made out of 3 parts (3 sixths of a
cup of water), and the
![]() cup of water is made out of 4 parts (4 sixths of a
cup of water is made out of 4 parts (4 sixths of a
cup of water), so the "little more" we were discussing above is just one of
those parts. Since
![]() cup is 3 parts, and
the "little more" is 1 part, the "little
cup is 3 parts, and
the "little more" is 1 part, the "little
more" is
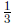 of the
of the
![]() cup of water.
This explains why
cup of water.
This explains why
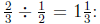 there's a
there's a
whole
![]() cup plus another
cup plus another
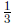 of the
of the
![]() cup in
cup in
![]() of a cup of water.
of a cup of water.
To recap: we are considering the fraction division problem
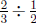 in terms
in terms
of the story problem "how many
![]() cups of water are in
cups of water are in
![]() of a cup of water?"
of a cup of water?"
If we give
![]() and
and
![]() the common
denominator of 6, then we can rephrase
the common
denominator of 6, then we can rephrase
the problem as "how many
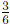 of a cup are in
of a cup are in
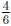 of a cup?" But in terms of
of a cup?" But in terms of
Figure ??, this is equivalent to the problem "how many 3s are in 4?" which
is the problem 4 ÷ 3, whose answer is
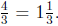 . Notice that
. Notice that
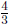 is exactly the
is exactly the
same answer we get from the "invert and multiply" procedure for fraction
division:
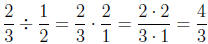
So the "invert and multiply" procedure gives the same
answer to
![]() that
that
we arrive at by using the "how many groups?" interpretation of division.
The same line of reasoning will work for any fraction division problem
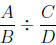
Thinking logically, as above, and interpreting
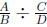 as "how many
as "how many
 cups
cups
of water are in
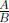 cups of water?", we can conclude that
cups of water?", we can conclude that
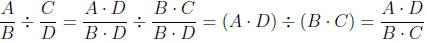
The final expression,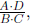 is the answer provided by the "invert and multiply"
is the answer provided by the "invert and multiply"
procedure for dividing fractions. Therefore we know that the "invert and
multiply" procedure gives answers to division problems that agree with what
we expect from the meaning of division.
Class Activity 0B: "How Many Groups?" Fraction Di-
vision Problems
Using the "How Many in One Group?" Interpretation
to Explain Why "Invert And Multiply" Is Valid
Above, we saw how to use the "how many groups?" interpretation of division
to explain why the "invert and multiply" procedure for fraction division is
valid. We can also use the "how many in one group?" interpretation for
the same purpose. This interpretation, although perhaps more difficult to
understand, has the advantage of showing us directly why we can multiply
by the reciprocal of the divisor in order to divide fractions.
Consider the following "how many in one group?" story problem for
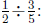
You used
![]() of can of paint to
paint
of can of paint to
paint
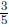 of a wall. How many cans
of a wall. How many cans
of paint will it take to paint the whole wall?
This is a "how many in one group?" problem because we can think of the
paint as " filling"
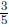 of the wall. We can also see that this is a
division problem
of the wall. We can also see that this is a
division problem
by writing the corresponding number sentence:
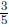 ·(amount to paint the whole wall) =
·(amount to paint the whole wall) =
![]()
Therefore
amount to paint the whole wall =![]()
We will now see why it makes sense to solve this problem
by multiplying
![]() by the reciprocal of
by the reciprocal of
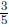 , namely by
, namely by
![]() . Let's focus on the
wall to be painted,
. Let's focus on the
wall to be painted,
as shown in Figure 2. Think of dividing the wall into 5 equal sections, 3 of
the 1/2 can of paint is divided equally
|
the 1/2 can of paint is divided equally among 3 parts |
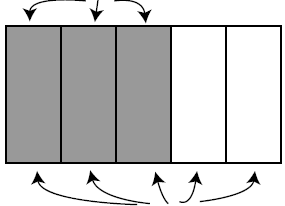 |
|
the amount of paint for the full wall is 5 times the amount in one part |
Figure 2: The Amount of Paint Needed for the Whole Wall is
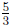 of the
of the
![]() Can
Can
Used to Cover
![]() of the Wall
of the Wall
which you painted with the
![]() can of paint. If you
used
can of paint. If you
used
![]() a can of paint to
a can of paint to
paint 3 sections, then each of the 3 sections required
![]() or
or
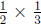 cans
cans
of paint. To determine how much paint you will need for the whole wall,
multiply the amount you need for one section by 5. So you can determine
the amount of paint you need for the whole wall by multiplying the
![]() can of
can of
paint by
![]() and then multiplying
that result by 5, as summarized in Table 1.
and then multiplying
that result by 5, as summarized in Table 1.
But to multiply a number by
![]() and then multiply it
by 5 is the same as
and then multiply it
by 5 is the same as
multiplying the number by
![]() . Therefore we can
determine the number of
. Therefore we can
determine the number of
cans of paint you need for the whole wall by multiplying
![]() by
by
![]() :
:
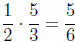
This is exactly the "invert and multiply" procedure for
dividing
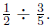 It
It
shows that you will need
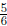 of a can of paint for the whole wall.
of a can of paint for the whole wall.
|
use
|
 |
use
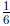 can paint for can paint for
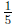 of the wall
of the wall |
 |
|
use
|
| in one step: |
|
use
|
 |
Table 1: Determining How Much Paint to Use for a Whole
Wall if
![]() Can of
Can of
Paint Covers
![]() of the Wall
of the Wall
The argument above works when other fractions replace
![]() and
and
![]() , thereby
, thereby
explaining why
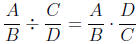
In other words, to divide fractions, multiply the dividend
by the reciprocal
of the divisor.

